План-конспект зачетного урока по математике, проводимого в 7 классе на тему: "Разложение разности квадратов на множители"

План-конспект урока математики, проводимого в 7 ”Б” классе.

Тема урока: “Разложение разности квадратов на множители”.

Дата: 22.04.2005 г.

Цели:

Образовательная: Создать условия для усвоения знаний и умений новой темы. Обеспечить повторение и обобщение материала. Рассмотреть способы разложения разности квадратов на множители, применяя формулу сокращенного умножения.

Развивающая: Способствовать формированию умений применять приемы обобщения, выделения главного, перенос знаний в новую ситуацию; развитию мышления, внимания и памяти.

Воспитательная: Содействовать вниманию интересов к новой теме, активности и умению общаться.

Тип урока: комбинированный урок;

Оборудование: мел, тряпка, доска.

План урока:

1.  Организационный момент (1-2 мин).

2.  Проверка домашнего задания (5 - 7 мин).

3.  Изложение нового материала (10-15 мин.)

4.  Закрепление нового материала (15-20 мин).

5.  Подведение итогов урока (2-3 мин.)

6.  Домашнее задание (1-2 мин.)

Ход урока:

1.  Организационный момент:

- приветствие;

- проверка готовности к уроку;

- проверка отсутствующих;

- объявление темы и целей урока;

2.  Проверка домашнего задания:

Объясняю ребятам то, что им было непонятно при выполнении домашнего задания. Отвечаю на их вопросы.

3.  Изложение нового материала:

Изложение материала начинаю с повторения квадратов натуральных чисел и формул сокращенного умножения. Сказанное мною число учащиеся должны возвести в квадрат и наоборот. Вызываю тех, кто поднимает руку.

а)  11²=121; 12²=144;13²=169; 14²=196; 15²=225;

На предыдущем уроке мы с вами применяли формулу произведения разности двух выражений на их сумму для представления произведений в виде многочленов. (Кто-нибудь из учеников помогает мне написать ее на доске (a-b)(a+b) = a² – b².) Теперь давайте рассмотрим формулу разности квадратов a² – b² = (a-b)(a+b). Если сравнить эти две формулы, то можно увидеть, что они отличаются друг от друга только порядком записи. Таким образом, сегодня мы должны научиться применять формулу разности квадратов при разложении на множители многочленов.

Далее, чтобы учащиеся немного усвоили материал, устно рассматриваем примеры из №912, №939, которые заранее выписаны на доске. В №939, прежде чем решать спрашиваю у ребят, квадраты каких чисел встречаются в примерах этого номера.

№912

в) (b – a)(b + a) = b² – a²;

з) (7+3y)(7 – 3y) = 49 – 9y²;

к) (2a – 3b)(3b + 2a) = 4a² – 9b²;

и) (n-3m)(3m+n) = n²-9m²;

№939

а) x² – y²  = (x – y)(x + y);

д) 16 – b²  = (4 – b)(4 + b);

з) y² – 0,09 = (y – 0,3)(y + 0,3);

к)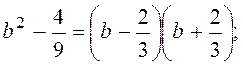

м)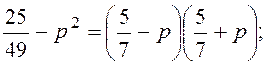

4.  Закрепление нового материала:

Переходим к решению задач по новой теме. Прежде, чем учащиеся приступят к самостоятельному решению задач, на доске подробно объясняю решение примеров

№940. Разложите на множители:

а)  25x² – y² = (5x)² – y² = (5x – y) (5x + y);

м)  16c²d² – 9a² = (4cd)² – (3a)² = (4cd – 3a) (4cd + 3a);

Остальные примеры ученики решают самостоятельно. Пункты б), в), г) решает ряд у окна, пункты д), е), ж) – средний ряд и пункты и), к) л) – третий ряд. Дав им, время подумать с каждого ряда вызываю по одному человеку. Далее всем классом разбираем ошибки, если таковы имеются.

б)  – m² +16n² = (4n)² – m² = (4n – m) (4n + m);

в)  36a² – 49 = (6a)² – 7² = (6a – 7) (6a + 7);

г)  64 – 25x² = 8² – (5x)² = (8 – 5x) (8 + 5x);

д)  9m² – 16n² = (3m)² – (4n)² = (3m – 4n) (3m + 4n);

е)  64p² – 81q² = (8p)² – (9q)² = (8p – 9q) (8p + 9q);

ж)  – 49a² + 16b² = (4b)² – (7a)² = (4b – 7a) (4b + 7a);

и)  9 – b²c² = 3² – (bc)² = (3 – bc) (3 + bc);

к)  4a²b² – 1 = (2ab)² – 1 = (2ab – 1) (2ab + 1);

л)  p² – a²b² = p² – (ab)² = (p – ab) (p + ab);

Далее решаем №942. Прежде, чем приступить к решению, на доске  подробно разбираю пункты a) и e).

№942. Вычислите:

а)  47² – 37² = (47 – 37)(47 + 37) = 10*84 = 840;

е)  ;

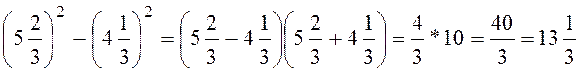Далее к доске вызываю трех человек. Один из них решает пример, проговаривая вслух.

б)  53² – 63² = (53 – 63)(53 + 63) = –10*116 = – 1160;

в)  126² – 74² = (126 – 74)(126 + 74) = 52*200 = 10400;

г)  21,3² – 21,2² = (21,3 – 21,2)(21,3 + 21,2) = 0,1*42,5 = 4,25;

д)  0,849² – 0,151² = (0,849 – 0,151)(0,849 + 0,151) = 0,698*1 = 0,698;

В №943 нужно разложить на множители либо числитель, либо знаменатель. После чего можно увидеть, что дробь можно сократить.

5.  Подведение итогов урока

Итак, сегодня на уроке мы познакомились со способом разложения на множители разности квадратов.

В оставшееся время выставляю оценки по результатам работы на уроке. 

6.  Задание домашнего задания

Домашнее задание: 3 – 4       № 939,

5 – 8       № 941, №944,

9 – 10     № 1045.