





Контрольная работа по математике №1, 11 класс (решения)
|
№ задания |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
A9 |
A10 |
|
№ правильного ответа |
4 |
3 |
4 |
1 |
1 |
1 |
4 |
2 |
2 |
1 |
B1. ![]() . Число
. Число ![]() составляет 100%, число 107 составляет
составляет 100%, число 107 составляет ![]() , тогда
, тогда 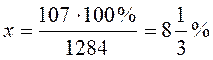 ,
, 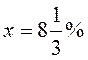 ,
, 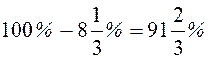 .
.
Ответ:
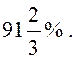
B2. По определению степени с дробным показателем имеем
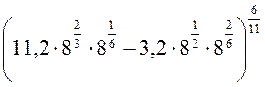 =
= 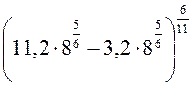 =
= 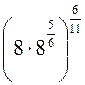 =
= ![]() .
.
Ответ: 8.
B3. Сухая масса цемента на складе составляет 100% – 16% =
84% от 800кг. смеси, то есть 672кг. Во время перевозки влажность
стала составлять 20 %, а сухая масса цемента составляет 80 % от привезенной
смеси. Массу привезенной смеси возьмем через x, тогда 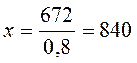 кг. Ответ:
840.
кг. Ответ:
840.
B4.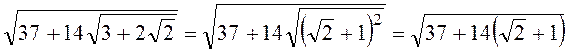 =
=![]()
![]() . Ответ:
. Ответ:
![]() .
.
B5. Перемножим первые две скобки по формуле разности квадратов,
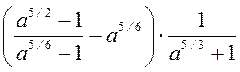 =
= 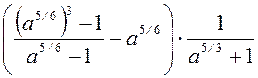 =
=
=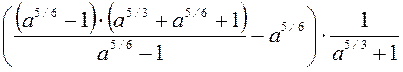 =
= 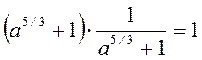 .
.
Ответ: 1.
B6.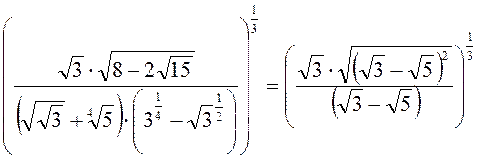 =
=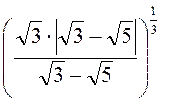 =
=![]() .
.
Ответ: ![]()
B7. Если система линейных уравнений не имеет решений, то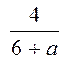
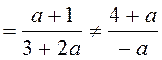 . Решим пропорцию
. Решим пропорцию 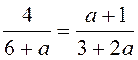 , получим
, получим ![]() . При
этом а = –2 не удовлетворяет неравенству:
. При
этом а = –2 не удовлетворяет неравенству: 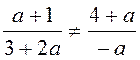 . Ответ:
3.
. Ответ:
3.
B8. Система линейных уравнений имеет бесчисленное
множество решений, значит,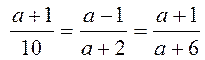 . Решим
. Решим 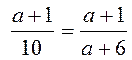 ,
, ![]() ; Равенство
; Равенство
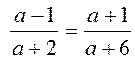 ; при
; при
![]() верно. Ответ:
4.
верно. Ответ:
4.
B9. Квадратный трехчлен принимает только положительные
значения, следовательно, 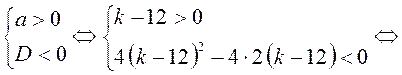
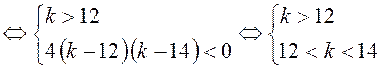 Ответ: 13.
Ответ: 13.
B10. Квадратное уравнение имеет два корня разных знаков, значит:
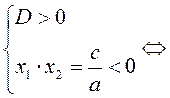
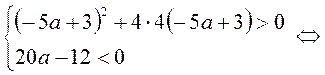
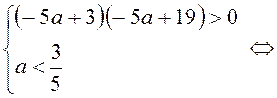
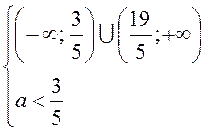 . Ответ:
. Ответ: ![]() .
.
B11. 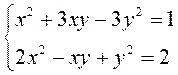
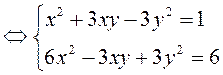 . Сложим уравнения системы, получим:
. Сложим уравнения системы, получим: ![]() ,
, ![]() .
Подставим найденные значения в первое уравнение, получим решения системы:
.
Подставим найденные значения в первое уравнение, получим решения системы: ![]() Ответ:
2.
Ответ:
2.
B12. ![]()
![]()
![]() . Тогда
. Тогда
![]() или
или![]() ,
, ![]() ,
, ![]() .
.
Находим
среднее арифметическое корней: 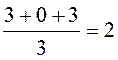 . Ответ:
2.
. Ответ:
2.
B13. Уравнение имеет положительные корни, следовательно,
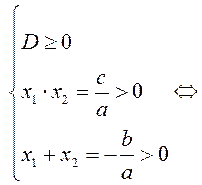
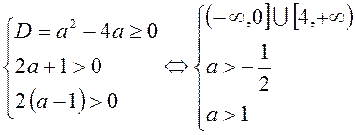 Ответ:
Ответ:
![]() .
.
B14. Пусть 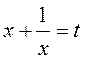 , тогда
, тогда 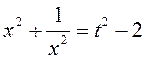 . Исходное уравнение примет вид:
. Исходное уравнение примет вид:![]() , откуда
, откуда 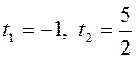 .
Тогда
.
Тогда 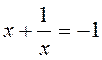 (D< 0, нет решений)
(D< 0, нет решений)
или
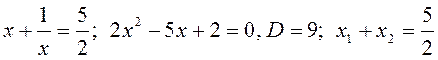 (по т. Виета). Ответ: 2,5.
(по т. Виета). Ответ: 2,5.
B15. Сгруппируем 1 и 4, 2 и 3 скобки, перемножим их, получим:
![]() . Введём новую переменную
. Введём новую переменную ![]() , тогда
, тогда ![]()
![]() ;
; ![]()
![]()
![]() ,
,![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Ответ:
-17; -3; ![]() .
.
B16. ![]() .
. ![]() Критические точки
функции
Критические точки
функции ![]() .Промежутки монотонности
функции [–3; –1] и [–1; 0]. Рассмотрим знаки функции на концах полученных
отрезков.
.Промежутки монотонности
функции [–3; –1] и [–1; 0]. Рассмотрим знаки функции на концах полученных
отрезков.
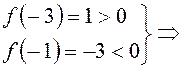 функция на промежутке [–3; –1] имеет один
корень.
функция на промежутке [–3; –1] имеет один
корень.
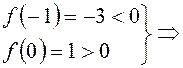 заданная функция на промежутке [–1; 0]
имеет один корень.
заданная функция на промежутке [–1; 0]
имеет один корень.
Значит, уравнение имеет на отрезке [–3; 0] два корня. Ответ: 2.
B17. ![]() ,
,
![]() ,
, ![]() .
.
![]() ,
, ![]() , сгруппируем
слагаемые первое с третьим,
второе с четвёртым и разложим на множители
, сгруппируем
слагаемые первое с третьим,
второе с четвёртым и разложим на множители ![]() . Критические
точки функции
. Критические
точки функции ![]() ,
, ![]() принадлежит
заданному отрезку
принадлежит
заданному отрезку
[0;
2]. Промежутки монотонности функции [0; 1] и [1; 2]. Находим знаки функции на концах
отрезков: 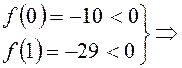 на этом промежутке функция не имеет
корней. Найдем знаки функции на концах следующего отрезка:
на этом промежутке функция не имеет
корней. Найдем знаки функции на концах следующего отрезка: 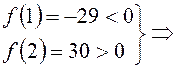
на отрезке [1; 2] функция имеет один корень. Ответ: 1.
B18. 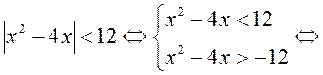
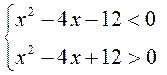 . Решив
неравенства, получим
. Решив
неравенства, получим 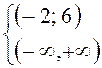 . Общее решение
. Общее решение ![]() .
.
Ответ: 14.
B19. ![]() .
D(f):
.
D(f): 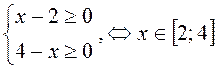 . Возведем в квадрат
обе части неравенства,
получим после упрощения
. Возведем в квадрат
обе части неравенства,
получим после упрощения ![]() ,чтоверно
для всех
,чтоверно
для всех
![]() .
.
Ответ: ![]() .
.
B20. Уравнение параболы в общем виде ![]() . По условию при
. По условию при ![]() . Подставим в уравнение, получим
. Подставим в уравнение, получим ![]() ,
,
![]() . Ответ:
. Ответ:
![]() .
.
B21.![]() .
Возводим в квадрат обе части уравнения
.
Возводим в квадрат обе части уравнения ![]() . Откуда
получим
. Откуда
получим
![]() Снова
возводим в квадрат обе части уравнения. После упрощения получим
Снова
возводим в квадрат обе части уравнения. После упрощения получим ![]() . Проверка подтверждает, что
. Проверка подтверждает, что ![]() – корень уравнения.
Подставим найденное значение x в заданное выражение. Ответ: 54.
– корень уравнения.
Подставим найденное значение x в заданное выражение. Ответ: 54.
B22. 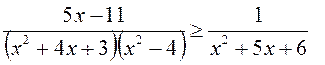 ,
,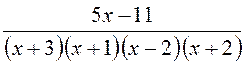 –
–
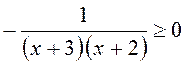 . После упрощения получим
. После упрощения получим 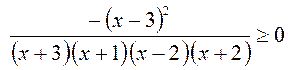 ,
,
x= 3 – решение неравенства. Последнее неравенство равносильно неравенству
![]() . Далее решаем методом интервалов.
. Далее решаем методом интервалов.
Ответ: 3.
B23. 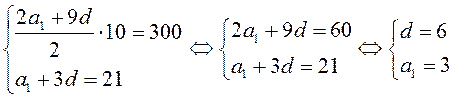 ,
,
![]() .
.
Ответ: 48.
B24. 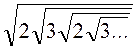 =
=![]()
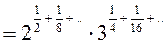 . Заметим, что показатели степеней
являются суммой бесконечно убывающей геометрической прогрессии, значит,
. Заметим, что показатели степеней
являются суммой бесконечно убывающей геометрической прогрессии, значит,
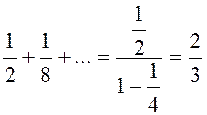 ;
; 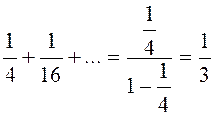 .
Окончательно получим
.
Окончательно получим
![]() . Ответ:
. Ответ:
![]() .
.
B25. ![]()
![]() – члены геометрической прогрессии, а
– члены геометрической прогрессии, а ![]() – члены арифметической прогрессии.
Используя характеристическое свойство той и другой прогрессии, запишем
– члены арифметической прогрессии.
Используя характеристическое свойство той и другой прогрессии, запишем 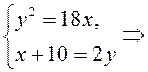
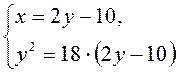 . Отсюда
. Отсюда ![]() (не удовлетворяет условию). Следовательно,
заданными числами будут: 2, 6 и 18. Сумма равна 26. Ответ:
26.
(не удовлетворяет условию). Следовательно,
заданными числами будут: 2, 6 и 18. Сумма равна 26. Ответ:
26.
C1. Область определения неравенства D(f):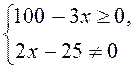 ,
, 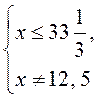 .
Исходное неравенство запишем в виде
.
Исходное неравенство запишем в виде 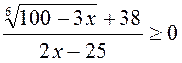 . Так как в области
определения числитель положителен, то
. Так как в области
определения числитель положителен, то ![]() ,
, ![]() . С учетом
. С учетом ![]() получим
решение неравенства
получим
решение неравенства 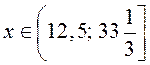 . Ответ:
. Ответ:
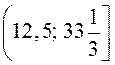 .
.
C2. По теореме Виета ![]() ,
, ![]() . Следовательно,
. Следовательно, ![]()
![]()
![]()
=![]() . Чтобы уравнение
. Чтобы уравнение ![]() имело
действительные различные корни, нужно, чтобы дискриминант
имело
действительные различные корни, нужно, чтобы дискриминант ![]() , то есть
, то есть ![]() ,
, ![]() ,
, ![]() ,
откуда
,
откуда ![]() . Функция
. Функция ![]() при
при ![]() принимает значения на интервале
принимает значения на интервале ![]() .
.
Ответ:
![]() .
.
C3. Сумма двух арифметических корней не может равняться
отрицательному числу, поэтому ![]() ,
, ![]() . (I) Запишем
данное уравнение в виде:
. (I) Запишем
данное уравнение в виде:
![]() или
или ![]() . (II) В
силу (I)
. (II) В
силу (I) ![]() . Уравнение (II)
принимает вид
. Уравнение (II)
принимает вид ![]() , откуда
, откуда ![]()
![]() ,
, ![]() .
Согласно (I)
.
Согласно (I) ![]() не является корнем
уравнения. Ответ:
4,25.
не является корнем
уравнения. Ответ:
4,25.
C4. Правая часть неравенства должна быть неотрицательной,
так как слева стоит сумма арифметических корней. Итак, ![]() ,
,
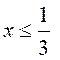 . (I) Неравенство
принимает вид
. (I) Неравенство
принимает вид ![]() ,
, ![]() , но
, но ![]() быть не может. Следовательно,
быть не может. Следовательно, ![]() ,
,
![]() ,
, ![]() ,
откуда
,
откуда ![]() . Учитывая (I), получим
. Учитывая (I), получим ![]() . Ответ:
. Ответ:
![]() .
.
C5. В точках пересечения графиков значения функций будут
равны, то есть ![]() .(I) Введем новую
переменную
.(I) Введем новую
переменную ![]() , где
, где ![]() , так
как
, так
как ![]() при
при ![]() , тогда
, тогда ![]() ,
, ![]() .
Уравнение (I) принимает вид
.
Уравнение (I) принимает вид ![]() или
или ![]() . (II) Возведем обе
части уравнения (II) в квадрат
. (II) Возведем обе
части уравнения (II) в квадрат ![]() или
или ![]() ,
, ![]() .
Проверкой убеждаемся, что
.
Проверкой убеждаемся, что ![]() – корень уравнения (II).
Так как
– корень уравнения (II).
Так как ![]()
![]() . Из уравнения
. Из уравнения ![]() найдем абсциссы точек пересечения:
найдем абсциссы точек пересечения: ![]() ,
, ![]()
![]() . Таким образом, координаты точек
пересечения графиков будут:
. Таким образом, координаты точек
пересечения графиков будут: ![]() и
и ![]() .
.
Ответ:
![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.