25. Расчетная подача пластинчатых гидромашин. Равномерность подачи
25.1. Подача двухпластинчатого насоса одинарного действия
Подача каждой пластиной за один
оборот определится площадью, отмеченной точечной штриховкой (рис. 6.1., б).
Эта площадь при угле ![]() и толщины пластины
и толщины пластины ![]() будет находиться по формуле:
будет находиться по формуле:
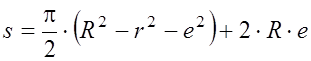 , где R
и r – радиусы статора и ротора.
, где R
и r – радиусы статора и ротора.
Следовательно, средняя расчетная подача насоса с
учетом, что за каждый оборот вытиснится два объема, соответствующих этой площади,
и учетом объема пластин (![]() ) будет равна:
) будет равна:
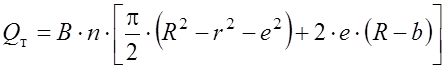
где В – ширина ротора;
n – частота вращения вала насоса;
b – толщина пластины.
Так как текущая площадь вытеснения в рассматриваемом двухпластинчатом насосе изменяется по углу поворота вала, переменной будет и подача. Наличие пульсации подачи и работа при небольших давлениях ограничивает применение насосов этой схемы.
25.2. Подача многопластинчатого насоса одинарного действия
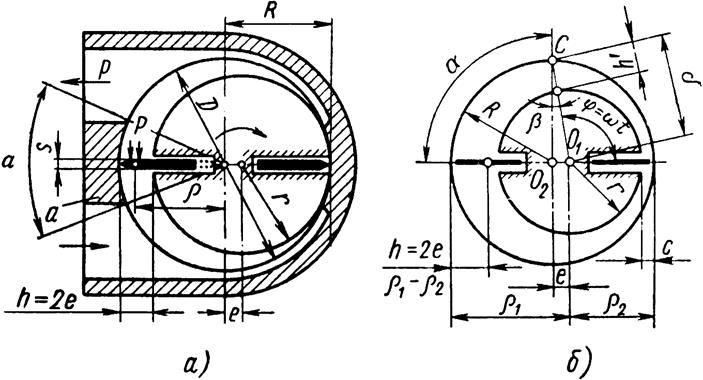
Рис. 6.4. – Расчетные схемы пластинчатого насоса
Рабочий объем q насоса равен объему,
описываемому рабочей частью пластины высотой ![]() ,
имеющей контакт с левой разделительной перемычкой а за один оборот (рис.
6.4, а; условно показаны лишь две пластины и рабочая высота правой
пластины принята равной нулю).
,
имеющей контакт с левой разделительной перемычкой а за один оборот (рис.
6.4, а; условно показаны лишь две пластины и рабочая высота правой
пластины принята равной нулю).
Допуская, что толщина пластины равна нулю и рабочая
высота ее при повороте ротора на угол ![]() , в
пределах которого пластина будет находиться в контакте с левой перемычкой а
статора, не изменяется и равна
, в
пределах которого пластина будет находиться в контакте с левой перемычкой а
статора, не изменяется и равна ![]() , находим рабочий объем
насоса:
, находим рабочий объем
насоса:
![]() , где ρ
– расстояние от центра вращения ротора до центра давления рабочей площади
пластины
, где ρ
– расстояние от центра вращения ротора до центра давления рабочей площади
пластины ![]() ;
;
B – ширина ротора,
D – диаметр колодца в корпусе статора.
Средняя расчетная (теоретическая) подача насоса в единицу времени с учетом толщины пластин, будет равна:
![]() .
.
25.3. Расчетная подача пластинчатого насоса двукратного действия
Пластина (рис. 6.3) при перемещении по концентричным
участкам между окнами а1 и b1 или а2 и b2 вытесняет объем Q',
по величине равный произведению площади рабочей части пластины ![]() на окружную скорость
на окружную скорость ![]() ее центра давления при рабочей высоте
пластины
ее центра давления при рабочей высоте
пластины ![]() :
:
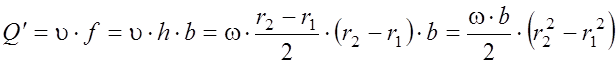 , где B
и h – ширина и высота рабочей части пластины;
, где B
и h – ширина и высота рабочей части пластины;
r2 и r1 – большой и малый радиусы статора;
ω – угловая скорость ротора.
Подставив значение ω и учитывая, что одновременно происходит вытеснение жидкости из двух камер, получим выражение для вычисления подачи насоса с учетом толщины пластин и их наклона (рис. 6.3, а):
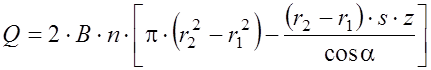 .
.
Для насосов с радиальным расположением пластин (рис. 6.3, б) подача определяется по формуле:
![]() .
.
Угол ![]() наклона пазов ротора
под лопасти к радиусу ротора обычно принимают равным 13–15° при малых диаметрах
ротора (до ~80 мм) и 7–8° при больших диаметрах.
наклона пазов ротора
под лопасти к радиусу ротора обычно принимают равным 13–15° при малых диаметрах
ротора (до ~80 мм) и 7–8° при больших диаметрах.
25.4. Регулирование подачи пластинчатого насоса
Регулирование производительности ![]() и изменение направления подачи
осуществляются соответствующим изменением величины и знака эксцентриситета е
(рис. 6.5). В положении I насос установлен на максимальный эксцентриситет
и изменение направления подачи
осуществляются соответствующим изменением величины и знака эксцентриситета е
(рис. 6.5). В положении I насос установлен на максимальный эксцентриситет ![]() , что соответствует максимальному расходу
, что соответствует максимальному расходу ![]() ; в положении II значения
; в положении II значения ![]() и
и ![]() ; и в
положении III имеет место максимальный эксцентриситет обратного
знака (
; и в
положении III имеет место максимальный эксцентриситет обратного
знака (![]() ) и соответственно – максимальная подача
противоположного направления (
) и соответственно – максимальная подача
противоположного направления (![]() ).
).
Эксцентриситет изменяется обычно с помощью винтового механизма или иных механических и гидравлических устройств.
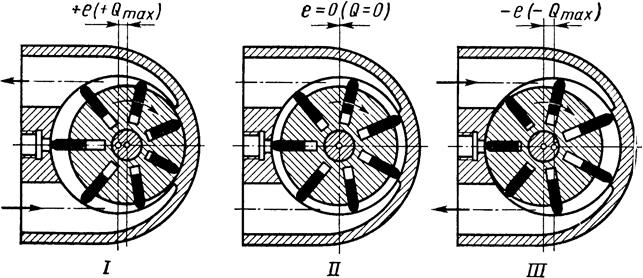
Рис. 6.5. – Схемы регулирования подачи пластинчатого насоса
Рабочий объем регулируемого насоса можно представить, введя безразмерное значение эксцентриситета:
![]() , где
, где
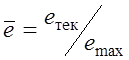 – относительный (безразмерный)
эксцентриситет, изменяющийся от 0 до ±1;
– относительный (безразмерный)
эксцентриситет, изменяющийся от 0 до ±1;
![]() и
и ![]() – максимальный
и текущий рабочие объемы;
– максимальный
и текущий рабочие объемы;
![]() и
и ![]() – максимальное и текущее значения
эксцентриситета.
– максимальное и текущее значения
эксцентриситета.
Расчётная подача регулируемого насоса определится по формуле:
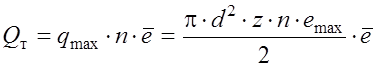 .
.
25.5. Равномерность (пульсация) подачи
Т.к. центр вращения ротора ![]() смещен
относительно центра кольца статора
смещен
относительно центра кольца статора ![]() , с диаметром
, с диаметром ![]() (рис. 6.4, б), принятое условие
(рис. 6.4, б), принятое условие ![]() будет справедливо только для среднего
относительно разделительной перемычки положения пластины, в иных же положениях
ее рабочая высота будет переменной.
будет справедливо только для среднего
относительно разделительной перемычки положения пластины, в иных же положениях
ее рабочая высота будет переменной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.