






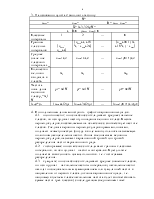

















меру случайных погрешностей, вызвавших разброс результатов измерений, обычно принимают среднее квадратическое отклонение s . Оценку s определяют по разбросу результатов измерений, которые служили для оценки истинного значения.
Величину средней квадратической погрешности измерений (стандарта) определяют по формуле …, а средней квадратической погрешности среднего арифметического – по формуле ….
Математический смысл
величины ![]() заключается в следующем. При проведении
большого количества серий опытов найденное в результате каждой серии значение
заключается в следующем. При проведении
большого количества серий опытов найденное в результате каждой серии значение ![]() распределяется около истинного значения по
закону, близкому к закону нормального распределения с дисперсией s2, мало отличающейся от
распределяется около истинного значения по
закону, близкому к закону нормального распределения с дисперсией s2, мало отличающейся от ![]() . При таком количестве опытов вероятность
того, что
. При таком количестве опытов вероятность
того, что ![]() , найденное в некоторой серии измерений,
будет отличаться от истинного значения не более
, найденное в некоторой серии измерений,
будет отличаться от истинного значения не более ![]() чем на
чем на ![]() , составляет 63,3 %; вероятность отклонения
меньше чем на
, составляет 63,3 %; вероятность отклонения
меньше чем на ![]() равна 94,4 % и т.д. Для
единственной серии опытов
равна 94,4 % и т.д. Для
единственной серии опытов ![]() служит полезной оценкой
количественного смысла не имеет. В этом случае для оценки наибольшего
возможного отклонения среднего арифметического
служит полезной оценкой
количественного смысла не имеет. В этом случае для оценки наибольшего
возможного отклонения среднего арифметического ![]() от
истинного значения х используют распределение Стьюдента. Величину
от
истинного значения х используют распределение Стьюдента. Величину ![]() можно принять в качестве абсолютной погрешности
среднего арифметического с вероятностью g.
можно принять в качестве абсолютной погрешности
среднего арифметического с вероятностью g.
Абсолютная
погрешность среднего арифметического ![]() независимых измерений
оценивается по формуле
независимых измерений
оценивается по формуле
![]()
Интервальной оценкой
измерений величины х является доверительный интервал ![]() , в которой попадает истинное значение с заданной
доверительной вероятностью g. Окончательный
результат измерений запишется в виде
, в которой попадает истинное значение с заданной
доверительной вероятностью g. Окончательный
результат измерений запишется в виде ![]() .
.
Относительная погрешность среднего арифметического
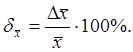
Пример. Спектрофотометрический анализ хинина сульфата в таблетках по 0,25 г при длине волны 234 нм дал следующие результаты: 99,9 %; 99,8; 99,6; 99,1; 99,2 и 99,2 %. Определить среднее значение и абсолютную и относительную погрешность при доверительной вероятности r = 0,95.
Решение. По формуле …,
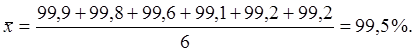
Оценка стандартного отклонения
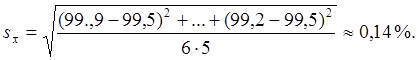
t0,95 (5) = 2,57. Абсолютная погрешность
![]()
![]()
Относительная погрешность
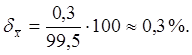 Истинное
содержание хинина сульфата в таблетках х=(99,5 ± 0,3) %.
Истинное
содержание хинина сульфата в таблетках х=(99,5 ± 0,3) %.
9.8. ОЦЕНКА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ КОСВЕННЫХ ИЗМЕРЕНИЙ.
Рассмотрим случай, когда искомая величина у связана с измеряемой величиной х (или несколькими измеряемыми величинами хi) известной функциональной зависимостью:
у = f(x1, x2, …, xi, …, xr).
Такие измерения называют косвенными.
Оценкой истинного значения у косвенно измеренной величины является среднее значение
![]()
![]()
где ![]() -
средние арифметические измеряемых на опыте величин x1,
x2,…, xr.
-
средние арифметические измеряемых на опыте величин x1,
x2,…, xr.
Оценкой среднего
квадратического отклонения является средняя квадратическая погрешность среднего
значения ![]() , вычисленная по формуле
, вычисленная по формуле
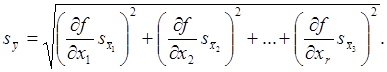
В этой формуле производные ![]() должны быть взяты в точках
должны быть взяты в точках ![]() , а
, а ![]() обозначают
средние квадратические погрешности средних значений измеряемых величин.
обозначают
средние квадратические погрешности средних значений измеряемых величин.
Абсолютная
погрешность ![]() среднего значения
среднего значения ![]() оценивается
по формуле
оценивается
по формуле
![]()
Интервальной оценкой
у является доверительный интервал ![]() , в
который попадает истинное значение косвенно измеренной величины у с
заданной доверительной вероятностью g.
Окончательный результат косвенно измеренной величины записывают в виде
, в
который попадает истинное значение косвенно измеренной величины у с
заданной доверительной вероятностью g.
Окончательный результат косвенно измеренной величины записывают в виде ![]() .
.
Относительная
погрешность среднего значения ![]()
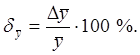
10. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТА:
Случайная величина Х имеет нормальное
распределение. при выборке объема n=15 выборочная средняя ![]() и исправленное среднее
квадратичное отклонение s=0,6.
Оценить неизвестное математическое ожидание при помощи доверительного интервала
с доверительной вероятностью 0,95.
и исправленное среднее
квадратичное отклонение s=0,6.
Оценить неизвестное математическое ожидание при помощи доверительного интервала
с доверительной вероятностью 0,95.
11. САМОКОНТРОЛЬ УСВОЕНИЯ ТЕМЫ:
Найти доверительный интервал для средней активности тетрациклина гидрохлорида с доверительной вероятностью 0,95 исходя из результатов серии измерений в пересчете на сухое вещество, представленных в табл
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.