чтобы оно было единственным, необходимо и достаточно, чтобы определитель системы не равнялся нулю.
Таким образом, чтобы система векторов была линейно независимой, необходимо и достаточно, чтобы не равнялся нулю определитель, в котором элементы столбцов есть координаты соответствующих векторов.
Пример 12. Определить, являются ли линейно независимыми векторы
![]()
Вычислим определитель, составленный из координат векторов a1; a2; a3:
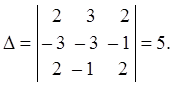
Так как Δ ? 0, данная система векторов — линейно независима. Если система векторов оказывается линейно зависимой, то в ней можно выделить линейно независимую часть векторов.
Линейно независимая часть системы векторов называется базисом этой системы. Число векторов в базисе системы называется рангом системы. (Ранг обозначают символом r.)
Пример 13.
Найти базис системы векторов ![]() ,
, ![]() ,
, ![]() .
.
Составим векторное уравнение
![]()
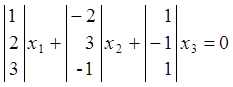 .
.
Решим это уравнение методом Гаусса:
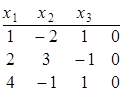
![]()
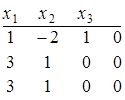
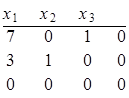
Таким образом, получим
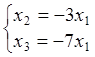 .
.
Базис
системы векторов ![]() составляют
векторы a2, a3, хотя им могла быть и любая другая пара линейно
независимых векторов данной системы. Ранг этой системы
составляют
векторы a2, a3, хотя им могла быть и любая другая пара линейно
независимых векторов данной системы. Ранг этой системы ![]() .
.
Рассмотрим систему n линейных уравнений с s неизвестными. В векторной форме она имеет вид (7). Сформулируем условия совместности и определенности системы (7).
1.
Система (7) совместна тогда и только тогда, когда ранги систем векторов ![]() и
и ![]() совпадают.
совпадают.
2.
Если ранг системы ![]() равен
числу неизвестных в системе (7), то есть
равен
числу неизвестных в системе (7), то есть ![]() ,
система имеет единственное решение.
,
система имеет единственное решение.
3.
Если ранг системы ![]() меньше
числа неизвестных
меньше
числа неизвестных ![]() ,
система имеет бесконечное множество решений.
,
система имеет бесконечное множество решений.
Пусть вектор k есть общее решение системы n линейных уравнений с s неизвестными. Это решение может быть представлено в форме
![]() ,
,
где ![]() — какое-либо частное
решение неоднородной системы уравнений.
— какое-либо частное
решение неоднородной системы уравнений.
![]()
— так называемая фундаментальная система решений однородной системы линейных уравнений, то есть исследуемой системы, в которой свободные члены полагаются равными нулю.
Общие свойства решения системы однородных линейных уравнений:
1) система всегда совместна
(Напомним, что всегда есть решение ![]() ,
причем это решение единственное, если определитель системы Δ ? 0. Если Δ = 0,
система имеет бесконечное множество решений.);
,
причем это решение единственное, если определитель системы Δ ? 0. Если Δ = 0,
система имеет бесконечное множество решений.);
2) сумма двух ненулевых решений есть также решение; произведение решений на любое число есть решение; таким образом, линейная комбинация нескольких решений есть также решение.
Бесконечное множество решений целесообразно упорядочить. Для этого из множества решений системы однородных уравнений следует выделить систему линейно независимых решений. Эта система и будет фундаментальной системой решений однородных уравнений.
Определение.
Фундаментальной системой решений называется совокупность векторов ![]() , являющихся линейно
независимыми решениями системы однородных уравнений, через которые линейно
выражается любое другое решение этой системы; при этом
, являющихся линейно
независимыми решениями системы однородных уравнений, через которые линейно
выражается любое другое решение этой системы; при этом
![]() ,
,
где ![]() — любые числа.
— любые числа.
Алгоритм построения фундаментальной системы решений:
1. Находят общее решение системы однородных уравнений.
2. Берут
систему ![]() — каких-либо линейно
независимых векторов размерности
— каких-либо линейно
независимых векторов размерности ![]() . Например, e1 = (1; 0; ...; 0); es–r = (0; 0; ...; 1).
. Например, e1 = (1; 0; ...; 0); es–r = (0; 0; ...; 1).
3. По общему решению находят значения разрешенных неизвестных, подставляя сначала вместо свободных
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.