Утверждены
Ученым советом
экономического факультета
5 марта 2001 г., пр. № 5
по написанию контрольных работ по дисциплине
Часть II
(контрольные работы № 4, 5, 6)
для студентов заочной формы обучения
(специальность — 060800 Экономика и управление на предприятии СКС)
Санкт-Петербург
2003
Составители:
доцент, кандидат технических наук Т. И. Башаратьян;
профессор, доктор технических наук С. А. Кабанов
доцент кафедры высшей математики Санкт-Петербургского университета авиаприборостроения, кандидат физико-математических наук И. А. Губкин
@ СПбГУП, 2003
 |
|||
 |
|||
Данная методическая разработка предназначена для студентов экономического факультета заочной формы обучения, выполняющих контрольные работы по дисциплине «Математика».
Самостоятельная работа — основная форма обучения студента-заочника. Важно правильно ее организовать. К организации обучения прежде всего относится умение работать с книгой. Для того чтобы ориентироваться в содержании, последовательности и объеме изучаемого материала, рекомендуется руководствоваться программой курса. Обязательно следует вести конспективную запись основных положений теории: определений, теорем, формул. Необходимо самостоятельно воспроизводить все этапы доказательств и математических выкладок. Только усвоив теоретическую часть и решив определенный объем задач по данной теме, можно приступать к выполнению контрольной работы.
Номера тем контрольных работ соответствуют их номерам в учебной программе. В каждой теме даются лишь фрагментарные пояснения основных положений, так как предполагается, что основной материал усвоен.
При оформлении контрольной работы следует указать тему, привести полностью условие задачи и далее подробно изложить ход решения, комментируя каждый этап и приводя подробные обоснования выбранных приемов. Работы, в которых эти требования не соблюдены, к рецензированию не допускаются. Решение по возможности следует доводить до ответа в общем виде и лишь затем выполнять вычисления. При оформлении контрольной работы рекомендуется сохранять последовательность задач полученного задания, писать решения подробно, аккуратно и разборчиво.
I. Определение. Пусть Х — множество числовых значений, принимаемых переменной х, У — принимаемых переменной у. Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Обозначают: y = f(x), y = y(x).
Множество Х называется областью определения функции; У — множеством значений функции. Эти множества часто обозначаются D(y), E(y).
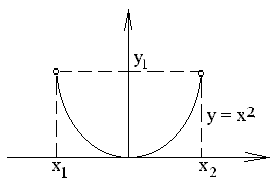
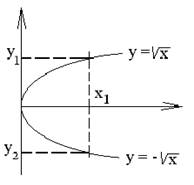
Рис. 1.
Заметим, что из
определения функции следует, что, например, у = х2 задает
функцию, уравнение же х = у2 соответствует, как видно из рис. 1, двум функциям: 
и
(появление двух функций связано с тем, что значение x1входит в две пары: x1; y1 и x1; y2).
II. Основные элементарные функции. (Их графики и свойства рекомендуем изучить самостоятельно.)
1. Целая рациональная функция (многочлен степени n или полином)
Частные случаи:
y = ax + b — линейная функция.
y = ax2 + bx + c — квадратичная функция.
2. Степенная функция
y = xn; n Î R.
3. Показательная функция
y = ax; a > 0; a ¹ 1.
4. Логарифмическая функция
y = logax; a > 0; a ¹ 1.
5. Тригонометрические функции.
6. Обратные тригонометрические функции.
III. Сложная функция. Пусть заданы две функции одной переменной y = f(y) и Y = g(x). Пусть множество G значений функции g(x) является подмножеством Y — области определения функции f. Функция y = f[g(x)] называется сложной функцией переменной х.
Сложную функцию называют также наложением или суперпозицией
функций. Например, 
— рассматривается как следующее
наложение элементарных функций
y = t2 ; t = ln |z| ; z = cos l ; l = x1/2.
Заметим, что наложение элементарных функций есть также элементарная функция.
Рекомендация. Очевидно, что большинство рассматриваемых в данном курсе функций порождаются наложением простейших элементарных функций, следовательно, необходимо досконально изучить свойства функций, перечисленных в п. II. При этом надо обратить внимание на такие характеристики функций, как их множества D(y) и E(y); точки пересечения с осями координат, четность или нечетность, периодичность, возрастание (убывание) на промежутках монотонности.
I. Предел числовой последовательности. Понятие предела одно из основных в математическом анализе. Это понятие лежит в основе дифференциального и интегрального исчислений — наиболее универсальных методов современной математики. Будем рассматривать предел числовой последовательности и предел функции.
Определение последовательности: пусть каждому натуральному числу поставлено в соответствие какое-либо число xn
х1, х2, …, xn, (1)
n Î N.
Последовательность (1) задает числовую последовательность. Такую последовательность называют также номерованной последовательностью.
Например: 1, 2, 4, 9 …
Очевидно, что любой член этой последовательности определяется по формуле xn = n2, xn — общий член последовательности.
Последовательность задана, если на множестве натуральных чисел указана формула общего члена xn, позволяющая по номеру n вычислять соответствующее значение xn.
Пусть xn = 3 — 10-n, тогда числовая последовательность имеет вид
3, 3 – 0,1, 3 – 0,01, 3 – 0,001…
Очевидно, что с увеличением n значение xn все больше приближается к 3. В этом случае говорят о пределе последовательности.
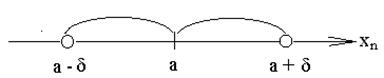
Определение предела последовательности. Число а называется пределом последовательности, если для любого положительного числа d найдется такой номер, равный n, начиная с которого будет выполняться условие
(2)
Считают: xn стремится к а, последовательность сходится к а.
Пишут: xn ® a; lim xn = a. Знак lim обозначает «предел» (от лат. limes — граница).
 |
Пример 1. Пусть 
.
Доказать, что 
.
Найти значение n, начиная с которого каждый член последовательности будет отличаться от своего предела меньше, чем на 0,01.
Решение: Докажем, что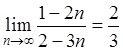 
.
По условию 
; d
= 0,01. В соответствии с (2) запишем и решим неравенство
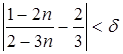Û
.
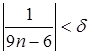Учитывая, что n Î N (следовательно,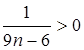 
) справедлива запись
. (1п)
Левая часть есть бесконечно малая величина, а правая часть
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.