Составление программы, вычисляющей величину мощности напряжения в электрической цепи

Министерство РФ по связи и информатике. СибГУТИ.

Курсовая работа по информатике.

Тема: «Напряжение в электрической цепи, определение мощности»

Выполнил: Студент гр. В-04.

Пономарев.Е.В.

Проверил: Рягин.Б.А.

Новосибирск 2011.

Задача к курсовой работе:

Напряжение в электрической цепи описывается уравнением:

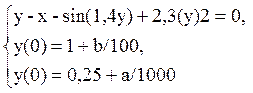
Составить программу, вычисляющую величину мощности (у²) в точках х=0.12, 0.22, 0.32, 0.42, 0.52, 0.62, 0.72, 0.82, 0.92.

Указания. Дифференциальное уравнение решить методом Рунге – Кутта на [0,1] с точностью до 10^-3 . значение функций в промежуточных точках находить линейной интерполяцией.

1) Цель курсовой работы:

а) рассчитать дифференциальное уравнение второго порядка методом Рунге – Кутта;

б) определить величину мощности (Y²) в точках X=0.12, 0.22, 0.32, 0.42, 0.52, 0.62, 0.72, 0.82, 0.92.

2) Краткое теоретическое введение:

Метод Рунге – Кутта:

Решение ищется на отрезке [a; b]. Для получения решения отрезок делится на m частей точками X_i =a+(b - a)*i/m с постоянным шагом h=(b - a)/m. Пусть y(x_i) - значение точного решения в точке x_i ; а y_i-значение приближённого решения в точке x_i.

В методе Рунге – Кутта на каждом шаге i используется четыре значения углового коэффициента по следующему правилу:

K1_i=F(X_i ; Y_i )=K_i;

K2_i=F(X_i + H/2 ; Y_i + K1_i*H/2);

K3_i=F(X_i + H/2 ; Y_i + K2_i*H/2);

K4_i=F(X_i + H ; Y_i + K3_i*H);

KC_i=(K1_i + 2*K2_i + 2*K3_i + K4_i)/6;

Y_i+1=Y_i + KC_i*H;

Единственная погрешность на каждом шаге i здесь такова R_i=Z_rk*Y⁽⁵⁾(C_i)*H⁵ X_i<C_i<X_i+1.

Суммарная погрешность характеризующая вычисления Y_n оценивается так:

Q=R_i*N | Y⁽⁵⁾(C_i)|=<M₅

Max|Q|<Z_rk*(b - a)M₅*H⁴

Получим другую формулу оценки суммарной погрешности с помощью двойного пересчёта:

Y(X_n)=Y_n + Z_rk*(b - a)M₅*H⁴=Y^h_n + M*H⁴

Y(X_n)=Y^h/2_n + M*(H/2)⁴ |*16

16*Y(X_n)=16*Y^h/2_n + M*H⁴

Y(X_n)=Y^h_n + M*H⁴

15*Y(X_n)=16Y^h/2_n – Y^h_n=15*Y^h/2_n + Y^h/2_n - Y^h_n

Y(X_n) – Y^h/2_n=(Y^h/2_n - Y^h_n ) /15

Если разность |(Y^h/2_n - Y^h_n)/15|<E, то |Y(X_n) – Y^h/2_n|<E.

Линейная интерполяция:

Пусть заданы значения Y_i =Y(X_i), при i=0, 1, 2, 3, …n, некоторой функции Y(X) в точках (узлах) X₀ X₁ X₂ … X_n , расположенных на отрезке [а,b], причем X₀ =a, X_n =b. Требуется приближенно востановить все значения Y(X) на отрезке[a,b] с помощью интерполяционного многочлена L_n (X) по правилу:

- в узлах X_i (I=0, 1, 2, 3,…,n): L_n(X_i)= Y_i

- вне узлов, для ХÎ(a,b) и Х¹ Х_i : L_n (Х)» Y(Х)

здесь n – порядок интерполяции, при n=1 рассматривается линейная интеполяция.

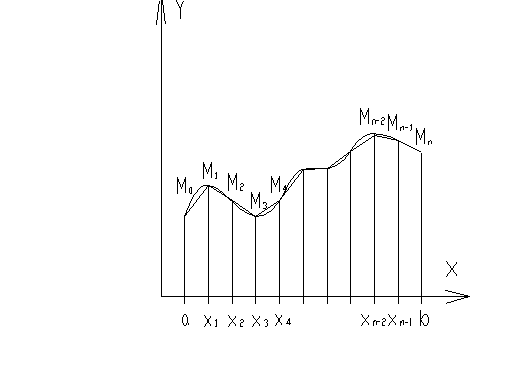
Каждые две соседние точки: М₀М₁, М₁М₂, М₂М₃,…,М_n-1М_n соединяем отрезком прямой  

Lⁱ₁= Y_i*(X - X_i+1)/( X_i - X_i+1) + Y_i+1(X - X_i)/( X_i+1 - X_i)

В совокупности все отрезки образуют ломаную линию М₀М₁М₂…М_n-1М_n, представляющую собой график интерполяционной кривой приближенно представляющей график искомой функции Y(X) на отрезке [a,b].

Чтобы вычислить L(X_k)»Y(X_k) в точке X_kÎ[a,b], нужно определить между какими узлами X_i и X_i+1 находится X_k, т.е. X_i£X_k<X_i+1 и определено выражение:

Lⁱ₁(X_k)= Y_i*( X_k - X_i+1)/( X_i - X_i+1) + Y_i+1(X_k - X_i)/( X_i+1 - X_i) »Y(X_k).

3) Описательная и операторная части программы

курсовой работы.

a, b – концы отрезка интегрирования;

e – погрешность счёта;

Y0 – начальное значение искомой функции;

file1.txt – файл, используемый для распечатки результатов;

PROCEDURE RK – процедура вычисления дифференциального уравнения второго порядка;

P – искомая мощность.

program cursovik;

uses crt, graph;

const a=0; b=1; e=0.001; y0=0;

type mas=array[0..2, 0..1000] of real;

k=array[1..2] of real;

var i, m, m2, i1, gt, gm, j : integer;

P, r1, r2, r3, r4, rc, x, x1, h, h1, min, max: real;

ff1 : text;

v, v1, v2 : mas;

{заданные функции}

function f1(x, y, y1 : real) : real;

begin f1:=sqr(x)/2-cos(1.4*y)*x+2.3*sqr(y1)*x; end;

function f2(x, y, y1 : real) : real;

begin f2:=x+sin(1.4*y)+2.3*sqr(y1); end;

{функции для графика}

function cx(x: real): integer;

begin cx:=round(10+(x-a)/(b-a)*300); end;

function cy(y: real): integer;

begin cy:=round(190+(y-min)/(min-max)*100); end;

{процедура Рунге-Кутта}

procedure rk(m : integer; var v1 : mas);

begin v1[1, 0]:=y0; h:=(b-a)/m;

for i:=0 to m-1 do begin

r1:=f1(a+i*h, v1[1, i], v1[2, i]);

r2:=f1(a+i*h+h/2, v1[1, i]+r1*h/2, v1[2, i]);

r3:=f1(a+i*h+h/2, v1[1, i]+r2*h/2, v1[2, i]);

r4:=f1(a+i*h+h, v1[1, i]+r3*h, v1[2, i]);

rc:=(r1+2*r2+2*r3+r4)/6;

v1[1, i+1]:=v1[1, i]+rc*h;

end; end;

{ Процедура вывода графика }

procedure gr(c, m2, j : integer; h, x: real);

begin

setcolor(c);

writeln(ff1);

for i:=1 to m2-1 do begin

line(cx(x), cy(v2[j, i]), cx(x+h), cy(v2[j, i+1]));

writeln(ff1, x :12:5, '   ', v2[j, i] :12:5);

x:=x+h;

end;

writeln(ff1, x :12:5, '   ', v2[j, m2] :12:5);

writeln;

end;

{начало программы}

begin

clrscr; m:=5;

assign(ff1, 'file1.txt'); rewrite(ff1);

repeat rk(m, v1);

m2:=2*m;

rk(m2, v2);

until abs(v2[1, m2]-v1[1,m])/15 < e;

{линейное интерполирование}

x:=a; x1:=0.02; h1:=0.1; i1:=1;

writeln(' Значения, полученные методом Рунге-Кутта ');

writeln(ff1, ' Значения, полученные методом Рунге-Кутта  ');

for i:=0 to m2 do begin

if (x1>=x) and (x1<=(x+h)) then

begin

v2[2, i1]:=v2[1, i+1]+(v2[1, i]-v2[1, i+1])*(x-x1)/h;

i1:=i1+1;

x1:=x1+h1;

end;

{ вывод значений, полученных методом Рунге-Кутта }

writeln('   ', x :3:3, '   ', v2[1, i] :3:3);

writeln(ff1, x :12:5, '   ', v2[1, i] :12:5);

x:=x+h;

end; writeln;

x:=0.12;

writeln(' Значения, полученные линейным интерполированием, искомая мощность.');

writeln(ff1, ' Значения, полученные линейным интерполированием, искомая мощность.');

for i:=1 to 10 do begin

P:=sqr(v2[2, i]);

writeln('   ', x :3:3, '   ', v2[2, i] :3:3, '   ', P :3:3);

writeln(ff1, x :12:5, '   ', v2[2, i] :12:5, '   ', P :12:5);

x:=x+h1;

end;

readln;

gt:=1; gm:=0;

initgraph(gt, gm, 'L:\bgi');

{сетка}

repeat

line(i, 5, i, 195);

i:=i+10;

until i>310;

i:=10;

repeat

line(5, i, 310, i);

i:=i+10;

until i>190;

{график}

min:=v[1, 0]; max:=min;

for i:=1 to m2 do begin

if v2[1, i] > max then max:=v2[1, i];

if v2[1, i] < min then min:=v2[1, i];

end;

writeln(ff1);

gr(1, m2, 1, h, a);

readln;

x1:=0.02;

writeln(ff1);

gr(2, 10, 2, h1, x1);

readln;

closegraph;

close(ff1);

end.

Значения, полученные методом Рунге-Кутта

X              Y

0.00000        0.00000

0.10000       -0.00483

0.20000       -0.01866

0.30000       -0.04048

0.40000       -0.06920

0.50000       -0.10370

0.60000       -0.14271

0.70000       -0.18482

0.80000       -0.22852

0.90000       -0.27215

1.00000       -0.31405

Значения, полученные линейным интерполированием, искомая мощность.

X              Y               P

0.12000       -0.00580        0.00003

0.22000       -0.02143        0.00046

0.32000       -0.04484        0.00201

0.42000       -0.07495        0.00562

0.52000       -0.11060        0.01223

0.62000       -0.15051        0.02265

0.72000       -0.19325        0.03734

0.82000       -0.23725        0.05629