Принятие инвестиционных решений в условиях неопределенности, страница 2

Рис. 5

Определение  уравнения регрессии с помощью графика

На основе указанных данных построена диаграмма (см. рис. 6)

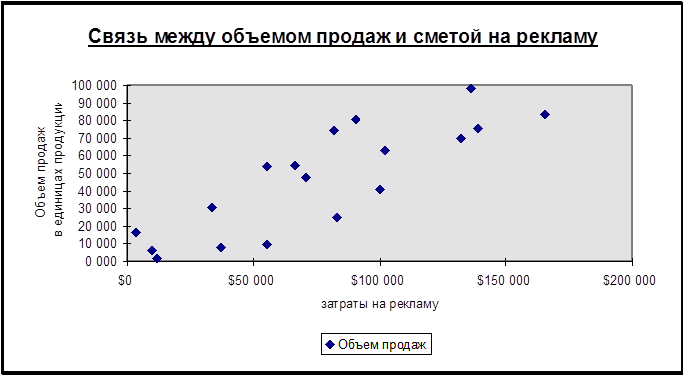
Рис. 6

Этот график может служить основой для проведения регрессионного анализа. Дальнейшие действия заключаются в следующем:

1.   Выполнить щелчок по графику для перехода в режим редактирования.

2.   Выбрать команду:

Диаграмма – Добавить линию тренда              (4)

3.   В диалоговом окне Линия тренда выбрать тип аппроксимации Линейная.

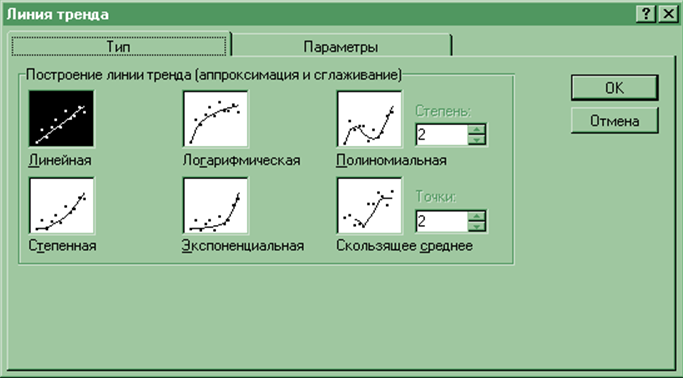
Рис. 7

4.   Перейти на вкладку Параметры и установить переключатели Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации (R^2).

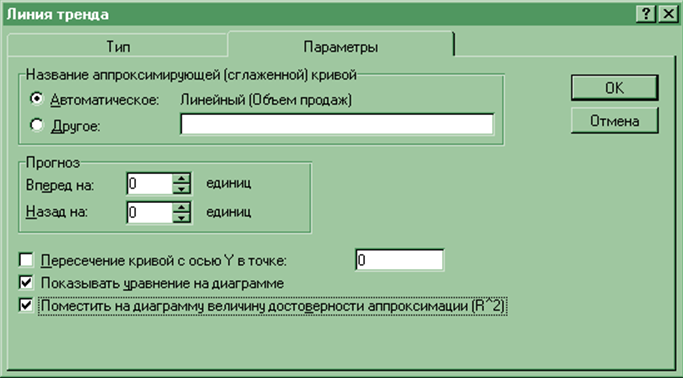
Рис. 8

В результате выполнения указанных действий будет построена линия тренда, определены уравнение регрессии и коэффициент детерминации (см. рис. 9).

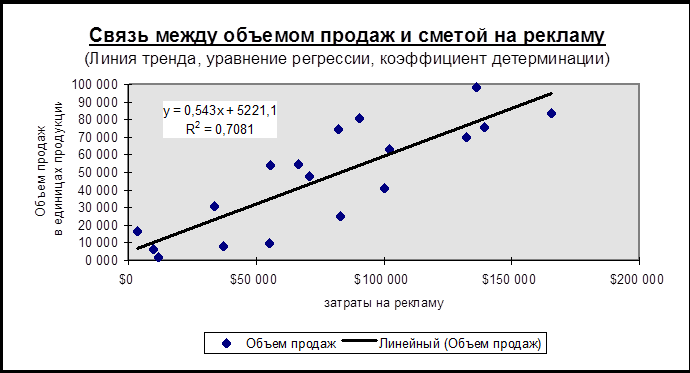
Рис. 9

Таким образом, по мере увеличения суммы затрат на рекламу объем продаж в единицах продукции также увеличивается.

Уравнение регрессии

                                                   (5)

показывает зависимость между денежной суммой, израсходованной на рекламу определенной продукции, и объемом продаж этой продукции.

R² –  коэффициент, отражающий меру точности определяемого уравнения регрессии. 

                                                                      (6)

Чем ближе R² к единице, тем  уравнение регрессии точнее описывает статистические данные.

Построение уравнения регрессии с помощью функции ТЕНДЕНЦИЯ

 Статистическая функция ТЕНДЕНЦИЯ вычисляет уравнение регрессии, используя линейную аппроксимацию. При необходимости это уравнение используется для предсказания новых значений.

ТЕНДЕНЦИЯ (известные_значения_y; известные_значения_x;                (7) новые значения_x; константа)

Стандартная ошибка определяется с помощью статистической функции

СТОШYX(известные_значения_y; известные_значения_x)               (8)

Величина, вычисленная с помощью этой функции, служит мерой ошибки предсказанного значения y для каждого значения x.

Построение уравнения множественной регрессии  с помощью Пакета анализа

Пример 3.

Предположим, кроме увеличения расходов на рекламу, исследуются последствия понижения цены на единицу продукции. На рис. 10 отображены смета на рекламу, показатели объемов продаж и цены различных товаров.

	A	B	C
1	Рекламный бюджет	Цена за шт.	Объем продаж
2	$3 500	$88	16 523
3	$10 073	$110	6 305
4	$11 825	$85	1 769
5	$33 550	$28	30 570
6	$37 200	$101	7 698
7	$55 400	$71	9 554
8	$55 565	$7	54 154
9	$66 501	$82	54 450
10	$71 000	$62	47 800
11	$82 107	$24	74 598
12	$83 100	$91	25 257
13	$90 496	$40	80 608
14	$100 000	$45	40 800
15	$102 100	$21	63 200
16	$132 222	$40	69 675
17	$136 297	$8	98 715
18	$139 114	$63	75 886
19	$165 575	$5	83 360

Рис. 10

Для использования Пакета анализа при проведении регрессионного анализа следует выбрать команду:

Сервис – Анализ данных(9)

В диалоговом окне Анализ данных надо выбрать инструмент анализа Регрессия.

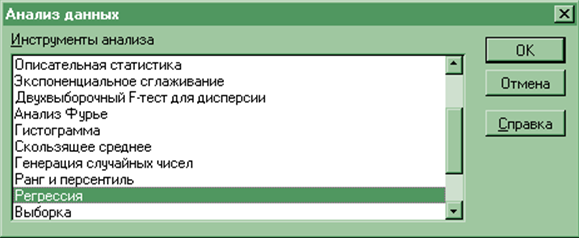
Рис. 11

На экране появится диалоговое окно Регрессия.

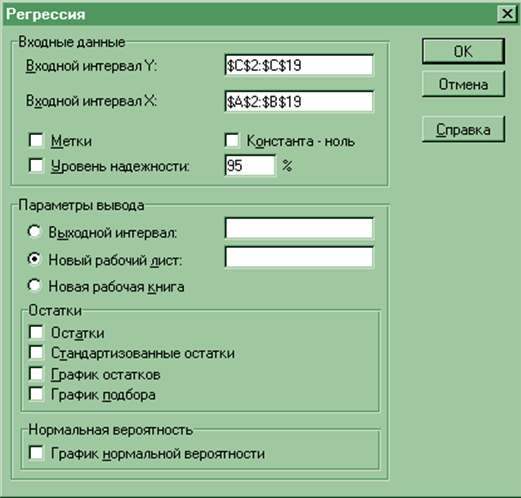
Рис. 12

В поле Входной интервал Y этого окна следует ввести ссылку на диапазон ячеек, содержащих данные об объеме продаж. В поле Входной интервал Х  надо указать ссылку на диапазон ячеек, включающих сведения о затратах на рекламу и ценах товаров.

Результаты, полученные с помощью инструмента Регрессия, показаны на рис. 13.