Проектирование привода к ленточному конвейеру (мощность на выходном валу – 0,3 кВт, число оборотов на выходном валу – 78 об/мин)

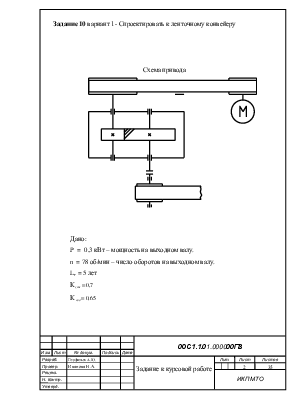
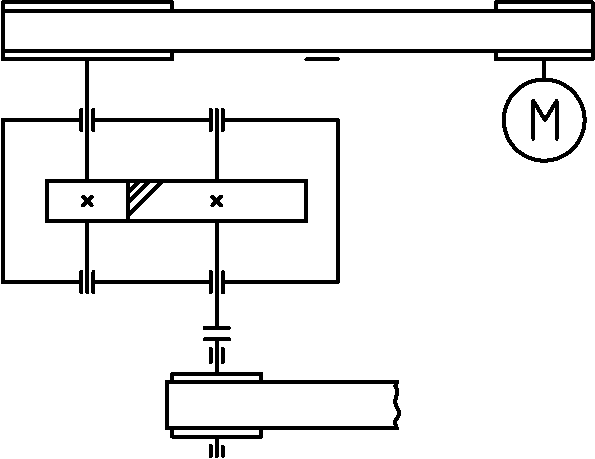
Задание 10 вариант 1- Спроектировать к ленточному конвейеру  

Схема привода

Дано:

P  =  0,3 кВт – мощность на выходном валу.

n  = 78 об/мин – число оборотов на выходном валу.

L_г = 5 лет

К 

К

1 Выбор электродвигателя и кинематический расчет

1.1 Определяем общий КПД привода

где:    η_оп = 0,96...0,98 – КПД открытой передачи

          η_зп = 0,96…0.97 – КПД закрытой передачи

η_м = 0,98 – КПД муфты

η_пк = 0,99…0,995 – КПД подшипников качения

η_пс = 0,98…0,99 – КПД подшипников скольжения

1.2 Требуемая мощность двигателя и частота

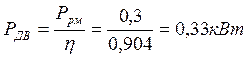
Выбираем трёхфазный асинхронный  двигатель 4АМ80А8У3 ТУ16-510.776-81 мощностью  0,37 кВт (Р_ном); частотой вращения 675 об/мин (n_ном).

1.3 Определяем передаточное число привода и его ступеней.

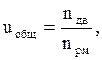
где:    n_дв – частота вращения двигателя, об/мин

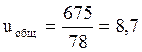
Распределив общее передаточное число принимаем:

u_оп=2,75 – передаточное число открытой плоскоременной передачи

u_зп= 3,15 – передаточное число цилиндрической передачи

1.4 Определим фактическое передаточное число

u_ф = u_оп· u_зп

u_ф=2,75 · 3,15 =8,7

1.5 Определяем мощности на валах привода, кВт:

1.6 Определяем частоты вращения на валах привода, об/мин:

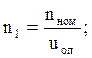
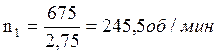
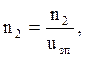
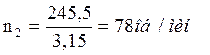
1.7 Определяем угловую скорость на  валах привода, рад/с

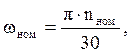
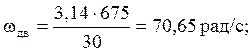
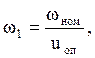
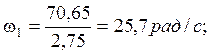
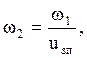
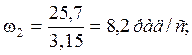
1.8 Определяем крутящие моменты на валах привода, Н·м

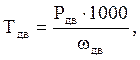
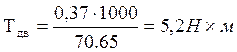
Т₁ = Т_дв × u_оп × η_оп × η_пк,

Т₁ =5,2 × 2,75 × 0,98 × 0,99 = 13,9 Н×м

Т₂ = Т₁× u_зп × η_зп × η_пк,

Т₂ = 13,9 × 3,15 × 0,97 × 0,99 = 42,05 Н×м

Т_рм = Т₂ × η_м × η_пс,

Т_рм = 42,05 × 0,98 × 0,99 = 40,8 Н×м

2 Расчет закрытой цилиндрической передачи

2.1 Выбор материалов зубчатой передачи

а) Определяем марку стали: для шестерни 40Х твердостью 470 НВ; для колеса – 40Х твердостью 300 НВ.

Разность средних твердостей НВ_1ср - НВ_2ср  ≥ 70

б) Механические свойства стали 40Х: для шестерни твердость – 470 НВ, термообработка улучшение + закалка ТВЧ; для колеса – 300 НВ, термообработка улучшение.

2.2 Определение допускаемых контактных напряжений для шестерни и колеса

а) Определяем коэффициент долговечности:

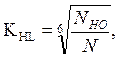
где N_HO – число циклов переменных напряжений, соответствующее пределу выносливости (для шестерни N_HO1= 68·10⁶ циклов, для колеса N_HO2 = 25·10⁶);

N – число циклов перемены напряжений за весь срок службы.

N = 573ωL_h , где ω – угловая скорость соответствующего вала, рад/с

L_h – срок службы привода, ч

L_h = 365LК_гt_сК_с , где L – срок службы привода, лет;

К_г – коэффициент годового использования;

t_с – продолжительность смены, час;

К_с – коэффициент сменного пользования.

L_h = 365 × 5 × 0,65 × 8 × 2 × 0,7 = 13286 ч для шестерни                 N₁ = 573 × 25,7 × 13286 = 195,7 · 10⁶ циклов для колеса                      N₂ = 573 × 8,2 × 13286 = 62,4 · 10⁶ циклов для шестерни                 т.к.    N₁ > N_HO1, то принимаем K_HL1=1

для колеса                      т.к.    N₂ > N_HO2, то принимаем K_HL2=1

б) Определяем допускаемое контактное напряжение [σ]_НО, соответствующее пределу контактной выносливости при числе циклов перемены напряжений N_HO :

для шестерни                 [σ]_НО1 = 14HRC_Эср +170

для колеса                      [σ]_НО2 = 1,8HВ_ср +67

[σ]_НО1 = 14 × 47 + 170 = 828 Н/мм²

[σ]_НО2 = 1,8 × 300 +67 = 540 Н/мм²

в) Определим допускаемые контактные напряжения для зубьев шестерни и колеса:

[σ]_Н1 = K_HL1[σ]_НО1 ;         [σ]_Н2 = K_HL2[σ]_НО2 ;

[σ]_Н1 =828 Н/мм²

[σ]_Н2  =540 Н/мм²

[σ]_Н =0,45([σ]_Н1 + [σ]_Н2)

[σ]_Н =0,45(828+540)=615,6 Н/мм² < 1,23[σ]_Н2 =664,2 Н/мм²

Следовательно                        [σ]_Н  = 615,6 Н/мм²

2.3 Определим допускаемые напряжения изгиба для зубьев шестерни[σ]_F1 и колес[σ]_F2

а)  Определим коэффициент долговечности:

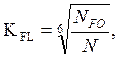
где N_FO  = 4 × 10⁶  - число циклов перемены напряжений для  всех сталей, соответствующее пределу выносливости;

N – число циклов перемены напряжений за весь срок службы (для шестерни N₁ = 195,7 · 10⁶ циклов, для колеса N₂ = 62,4 · 10⁶ циклов);

Т.к. N₁ > N_FO1 и N₂ > N_FO2 , то  K_FL1=1, K_FL2=1

б) Определяем допускаемое напряжение изгиба [σ]_FО, соответствующее пределу изгибной выносливости при числе циклов перемены напряжений N_HO :

[σ]_FО1 = 310 Н/мм² , в предположении что m<3мм;

[σ]_FО2 = 1,03НВ_ср2 = 1,03 × 300 = 309 Н/мм² ;

в) Определим допускаемые напряжения изгиба:

[σ]_F1 = K_FL1[σ]_FО1 ;           [σ]_F2 = K_FL2[σ]_FО2 ;

[σ]_F1 = 1 × 310 = 310 Н/мм² ;

[σ]_F2 = 1 × 309 = 309 Н/мм²

Для расчета будем пользоваться меньшим напряжением [σ]_F = 309 Н/мм²

2.4 Расчет закрытой цилиндрической передачи

2.4.1 Проектный расчет а) Определяем главный параметр – межосевое расстояние:

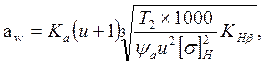
где: K_a–вспомогательный коэффициент (для косозубых передач K_a=43);

u – передаточное число редуктора или открытой передачи;

Т₂ – вращающий момент на тихоходном валу редуктора или на приводном валу рабочей машины для открытой передачи, Н·м;

Ψ_а=b₂/a_w – коэффициент ширины венца колеса (Ψ_а=0,28…0,36);

[σ]_H – допускаемое контактное напряжение колеса с менее прочным зубом или среднее контактное напряжение, Н/мм²;

К_Нβ – коэффициент неравномерности нагрузки по длине зуба (К_Нβ=1 )

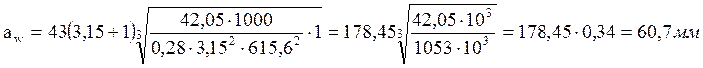
Полученное значение межосевого расстояния округлим до ближайшего значения из ряда нормальных линейных размеров a_w = 60 мм.

2.4.2 Определим модуль зацепления:

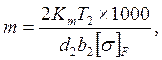
где: K_m – вспомогательный коэффициент (для косозубых передач K_m=5,8)

d₂=(2a_w u)/( u+1) =(2·60·3,15)/(3,15+1)= 91 мм – делительный диаметр колеса;

b₂= Ψ_аa_w=0,28·60 = 16,8 мм – ширина венца;

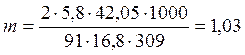мм

Полученное значение модуля округлим до стандартного из ряда чисел: m = 1 мм.

2.4.3 Определяем угол наклона зубьев (β_sin):

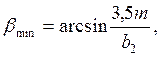
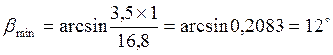
2.4.4 Определяем суммарное число зубьев шестерни и колеса:

Принимаем z_Σ  равным 117;

2.4.5 Уточним действительную величину угла наклона зубьев для косозубых передач:

2.4.6 Определим число зубьев шестерни:

Принимаю z₁ = 28

2.4.7 Определим число зубьев колеса:

2.4.8 Определим фактическое передаточное число (u_ф) и проверим его отклонение  (∆u) от заданного (u):

u_ф = z₂/z₁;    u_ф = 89/28=3,18;

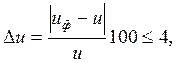
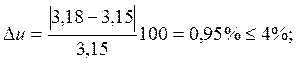
2.4.9 Определим фактическое межосевое расстояние:

a_w = (z₁+z₂) m / (2cosβ),

a_w = (7+20) 2 / (2×0,975) = 60 мм;

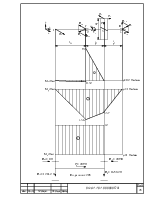
2.4.10 Определим основные геометрические параметры передачи:

Делительный диаметр шестерни:

d₁ = m z₁  / cosβ ;

d₁ = 1 × 28 / 0,975 = 28,7 мм;

Делительный диаметр колеса: 

d₂ = m z₂ / cosβ ;

d₂ = 1 × 89 / 0,975 = 91,3 мм;

Диаметр вершин зубьев шестерни:

d_а1 = d₁+2m ;

d_а1 = 28,7 + 2×1 =30,7мм;

Диаметр вершин зубьев колеса:

d_а2 = d₂+2m ;

d_а2 = 91,3 + 2×1 =93,3 мм;

Диаметр впадин зубьев шестерни:

d_f1 = d₁ – 2,4m;

d_f1 = 28,7 – 2,4×1 = 26,3 мм;

Диаметр впадин зубьев колеса:

d_f2 = d₂ – 2,4m;

d_f2 = 91,3 – 2,4×1 = 88,9 мм;

Ширина венца шестерни:

b₁ = b₂ + (2…4);

b₁ = 16,8 + 4 = 20,8 мм;

Ширина венца колеса:

b₂ = ψ_a × a_w ;

b₂ = 0,28 × 60 = 16,8 мм;

2.5 Проверочный расчет

2.5.1 Проверим межосевое расстояние:

a_w = (d₁ + d₂)/2;

a_w =(28,7 + 91,3) / 2 = 60 мм;

2.5.2 Проверим пригодность заготовок колес:

D_заг≤D_пред ;

D_заг1 = d_а1 + 6 = 30,7 + 6 = 36,7 мм ≤  200 мм ;

D_заг2 = d_а2 + 6 = 93,3 + 6 = 99,3 мм ≤  200 мм ;

S_заг≤S_пред ;

S_заг = b₂ + 4 = 8 + 4 = 12 мм≤125 мм ;

2.5.3 Проверим контактные напряжения:

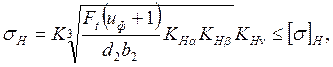
где:    К– вспомогательный коэффициент (для косозубых передач K=376);

F_t = (2T₂ * 10³) / d₂ = (2*42,05 *10³ ) / 91,3 = 921 Н – окружная сила в зацеплении;

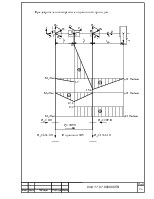
К_Нα – коэффициент, учитывающий распределение нагрузки между зубьями (для косозубых передач определяется по графику в зависимости от окружной скорости колес υ = (ω₂d₂) / 2000 = (8,2*91,3) / 2000