Вычисление инерционно-массовых характеристик турбокомпрессора

1. Постановка задачи.

Рассматривается переходной режим работы турбокомпрессора.

Схема:

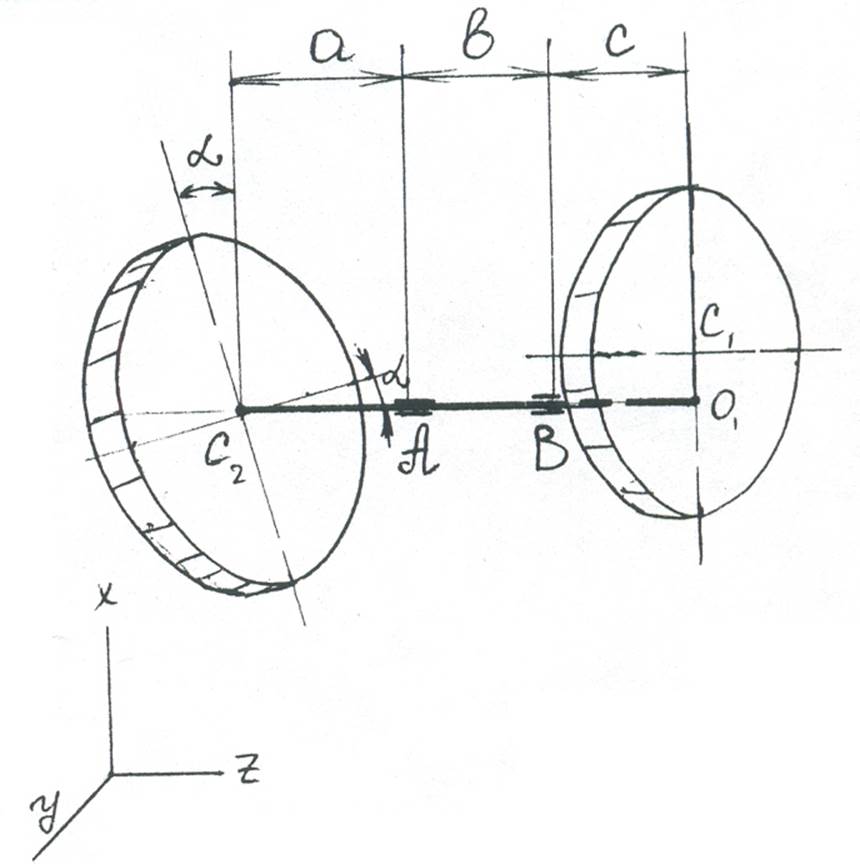
Исходные данные:

Физико-математическая модель:

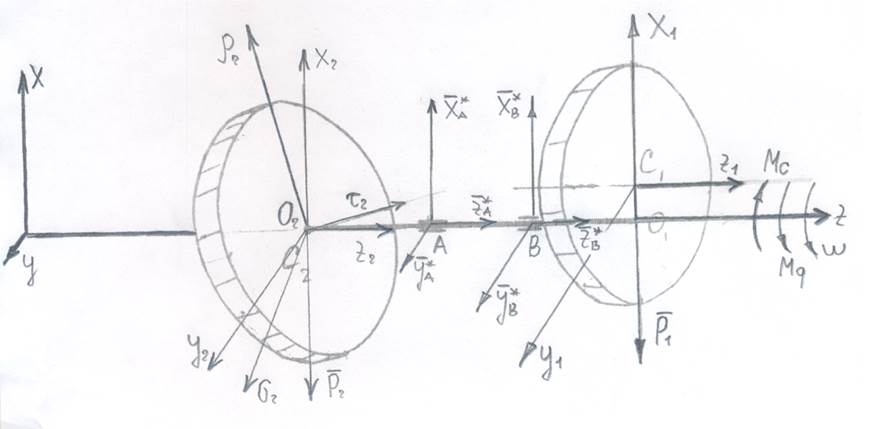
Воспользуемся теоремами об изменении количества движения и кинетического момента относительно точек А и В:

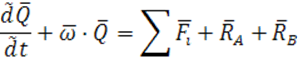
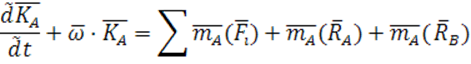
Кинетические моменты:

Момент привода:

Момент сопротивления:

2. Вычисление инерционно - массовых характеристик турбокомпрессора.

 Массу турбокомпрессора определяем как сумму его элементов:

Координаты центра масс элементов в системе координат OXYZ:

Координаты центра масс турбокомпрессора:

  

  

  

Далее вычисляем моменты инерции турбокомпрессора, относительно связанной с ним системы координат OXYZ, т.е. определим матрицу составляющих тензора инерции:

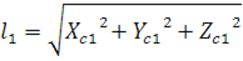
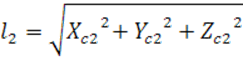
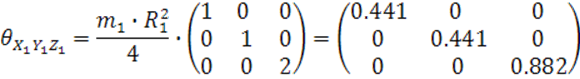
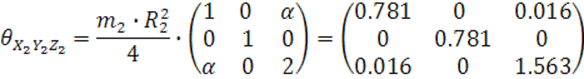
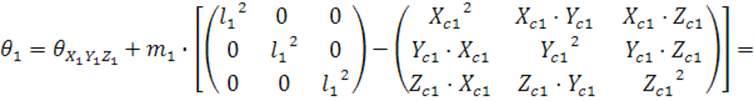
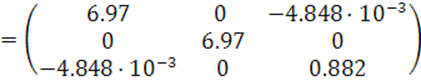
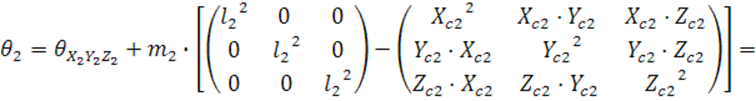
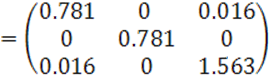
Матрица инерции турбокомпрессора:

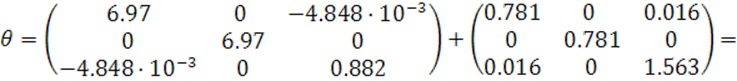
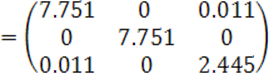
Выписываем все моменты инерции турбокомпрессора:

3. Составление уравнений движения.

Дифференциальное уравнение вращательного движения турбокомпрессора и уравнения для определения динамических реакций в подвижных осях имеют вид:

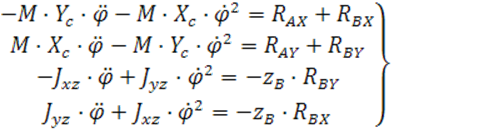
Преобразуем все уравнения и получим:

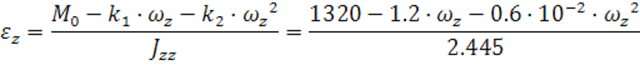
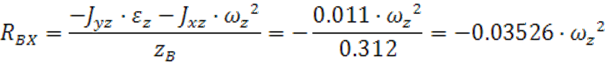
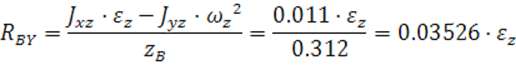
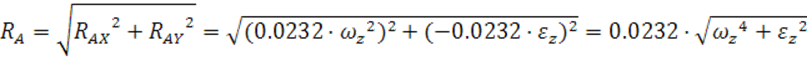
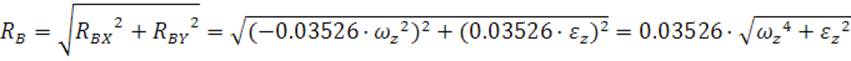
Найдем угловую скорость установившегося вращения ()

Решим это уравнение в маткаде и получим следующие результаты: , но  тогда

4. Таблица результатов.

Все последующие вычисления производились в маткаде. Распишем только ход решения:

·  Найдем производные:   ; ; ; ; ; ;

·  Вычислим все значения ( при времени  и задаем их в матрицу:

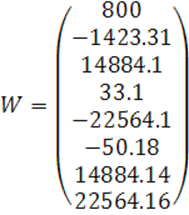
·  Задаем функцию: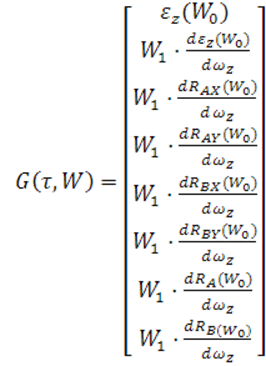

·  Задаем время   и количество шагов

·  Задаем функцию:   

И мы получаем следующую таблицу результатов:

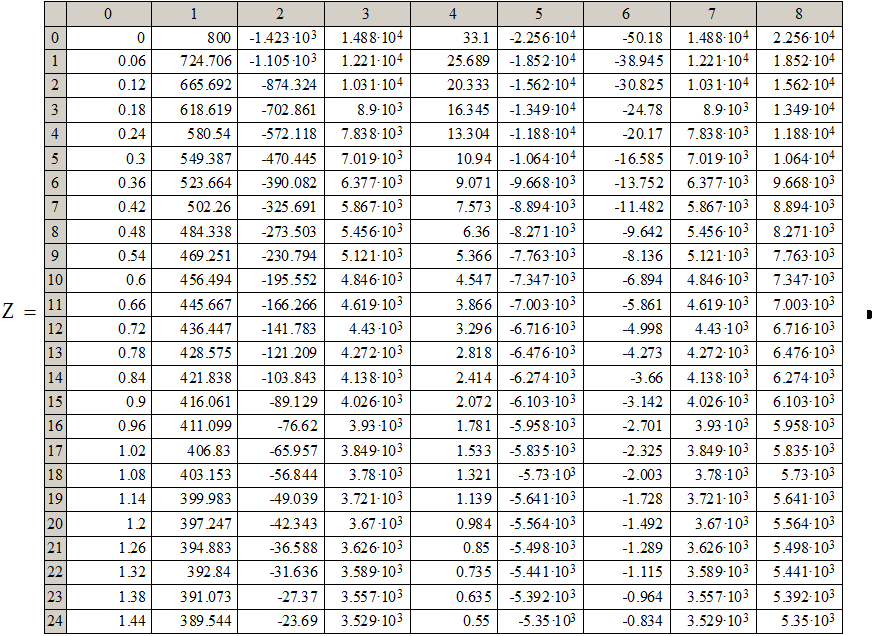
5. Построение графиков.

График  :

График  :

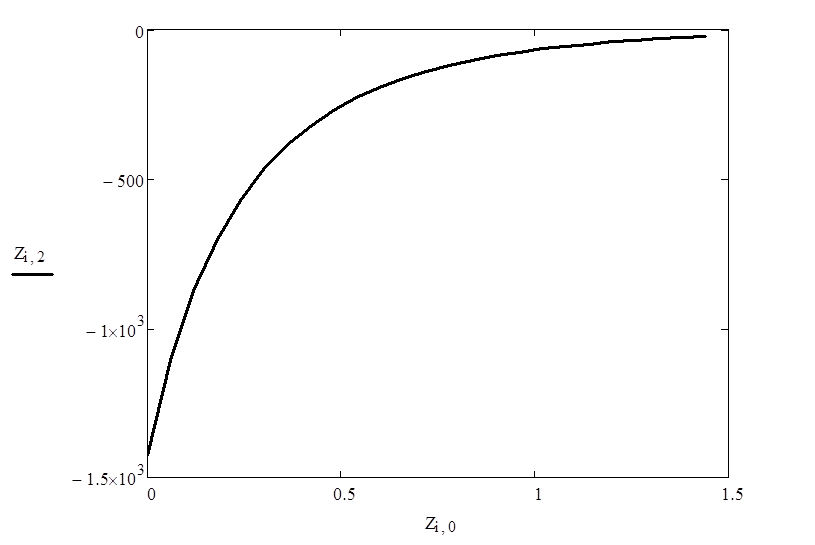
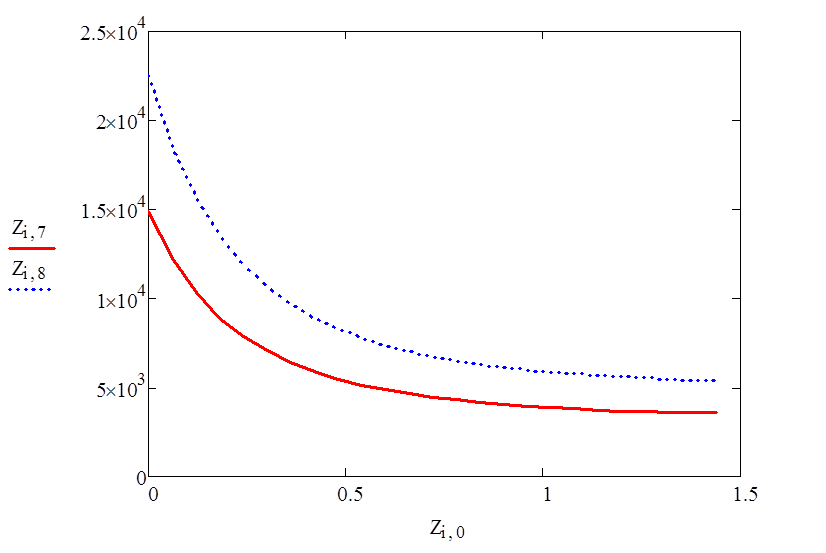
Графики  :