

Решение 5.110 с.1
Список используемых определений
· Оптическая длина пути:
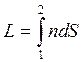 .
.
Для однородной среды:
![]() .
.
· Оптическая разность хода – разность оптических длин путей, проходимых волнами:
![]() .
.
· Интенсивность волн – модуль среднего по времени значения плотности потока энергии:
![]() ~
~![]() .
.
Суммирование амплитуд
элементарных колебаний, приходящихся в точке![]() , можно
произвести графически.
, можно
произвести графически.
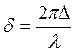 (1)
(1)
Решение:
|
|

 Нарисуем
спираль Френеля для 1,5 зон.
Нарисуем
спираль Френеля для 1,5 зон.
|
что соответствует сдвигу по фазе на:
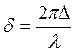 (1)
(1)
Рис.1
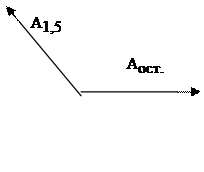
Рис.2
Решение 5.110 с.2
и повороту![]() на этот угол против часовой стрелки. Для
получения максимальной интенсивности нужно, чтобы
на этот угол против часовой стрелки. Для
получения максимальной интенсивности нужно, чтобы ![]() был
сонаправлен с
был
сонаправлен с ![]() .Для этого
.Для этого![]() следует
повернуть на угол:
следует
повернуть на угол:
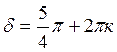 (к = 0,1…).
(3)
(к = 0,1…).
(3)
Из (1):
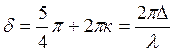 (4)
(4)
Заменим Δ на (2):
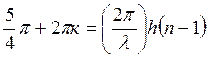 (5), следовательно:
(5), следовательно:
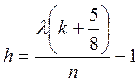 (6)
(6)
![]()
n = 1,5 (стекло)
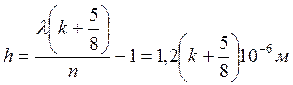 (7)
(7)
к = 0,1,2...
Ответ: 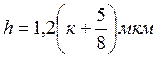
к = 0,1,2...
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.