Оптические спектры атомов водорода и ртути. Определение длин волн серии Бальмера в спектре атома водорода, страница 2

Длину волны любой спектральной линии можно представить через разность термов двух стационарных состояний

В этом состоит комбинационный принцип. Ему можно дать также Другую Формулировку. В спектроскопии принято характеризовать спектральные линии волновым числом   ν*₁=1/λ . Тогда если известны волновые числа ν*₁ и ν*₂    двух спектральных линий одной и той же серии, то их разность будет также волновым числом ν*₃  спектральной линии, принадлежащей тому же атому. Пусть, например, ν*₁=T₁-T₂    и ν*₂ = T₂-T₃   - волновые числа двух линий серии Лаймана. Тогда их разность

является волновым числом первой линии серии Бальмера.

Абсолютная величина энергии |E_n| стационарного уровня n-называется энергией связи электрона в атоме и может быть определена через термы как

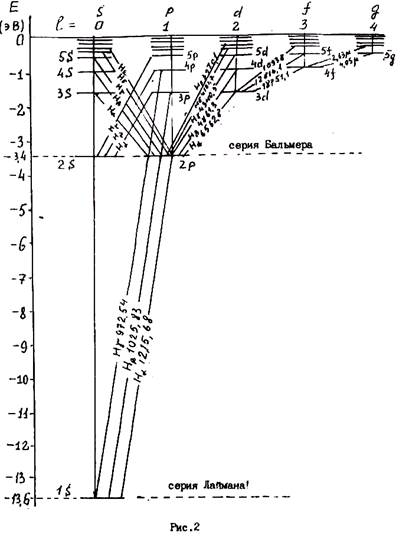
анергия  E_i ,   неооходимая для отрыва электрона от ядра, называется энергией ионизации и равна энергии связи для основного уровня с

n = I

Уравнение Юредингера (I) не отражает всех аспектов спектроскопии атома. При применении спектральных приборов с большой разрешающей способностью было обнаружено, что некоторые спектральные линии атома водорода расщепляются на две компоненты (являются дублетами). Это явление получило название тонкой структуры. Расщепление спектральных линий связано с расщеплением энергетических уровней, которое обусловлено наличием у электрона спина собственного механического момента импульса М_c .  Спин не связан с движением электрона в пространстве, как механический орбитальный момент импульса M_l ,   а является неотъемлемым свойством электрона таким же, как масса и заряд. Величина спина определяется по общим законам квантовой механики спиновым квантовым числом  S,    равным 1/2

Проекция спина М_sz на направление внешнего магнитного поля, так же как и проекция орбитального момента импульса М_lz  может принимать лишь квантованные значения, отличающиеся друг от друга на ħ

где m_c=±S=±1/2  - магнитное спиновое квантовое число. Полный момент импульса электрона M_j представляет собой сумму М_l и М_с Сложение моментов осуществляется по квантовым законам. Ряд важных результатов может быть получен с помощью векторной модели. Она представляет собой совокупность правил, позволяющих получать результаты, справедливость которых подтверждается строгими квантовомеханическими расчетами. Согласно векторной модели,механические (и магнитные) моменты изображаются в виде направленных отрезков и складываются по правилу параллелограмма (рис.3). Так как механическим моментам импульсов соответствуют магнитные моменты, а последние взаимодействуют между собой подобно двум контурам с током (это взаимодействие называется

с п и н - о р б и т а л ь н ы м), то М_l и M_s прецессируют относительно М_j , как два связанных механических гироскопа прецессируют относительно направления своего полного момента импульса.                       

При этом учитывается, что

1) углы между M_l и М_s должны быть такими, чтобы выполнялись условия квантования  M_ez=m_eħ  и M_sz=m_sħ

2) величина М_j может принимать лишь дискретные значения

квантовое число полного момента импульса.

Обусловленное спином расщепление энергетических уровней является релятивистским эффектом. Расстояние между уровнями тонкой структуры водородного атома может быть рассчитано по формуле

где j = l + s   l+s-1; … ; 0 ; … ; |l-s|+1 ; |l-s|  - постоянная тонкой структуры.

Она представляет собой квадрат элементарного заряда, выраженный в естественных единицах. (В естественной системе единиц за единицу массы принята масса электрона  , эа единицу длины - комп-тоновская длина волны электрона за единицу энергии - энергия покоя электрона

Спектры излучения атомов второй