Изучение вращательного движения твёрдого тела вокруг неподвижной оси на примере маятника Обербека

Министерство общего и профессионального образования

Обнинский Государственный Технический Университет Атомной Энергетики

Кафедра общей и специальной физики

Лабораторная работа № 6.

Тема:

«Изучение  вращательного  движения  твёрдого  тела  вокруг  неподвижной  оси  на  примере  маятника  Обербека».

Выполнил:   Головнёв Олег

Группа:         КИП-1-02

Проверил:   Мастеров  Виктор  Сергеевич.

Обнинск 2002.

Цель  работы: 

1. Экспериментально  проверить  основное  уравнение  вращательного  движения,  определить  момент  инерции  системы  и  оценить  влияние  момента  сил  трения.
2. Проверить  теорему  Штейнера.

Приборы:  маятник  Обербека.

Dt_сист = 0,0005с,  DM_сист = 0,0006кг,  Dr_сист = 0.002м,  Dh_сист = 0,0015м,  DP_сист = Dl_сист = 0,00005м.

а =;    

b = ;    db = ;  Db = b*db;

N = M*r*(g – a);   dN = ;   DN = N*dN;

N_тр = 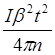;  n = 35;(2сл)  N_тр = 0,0011 Н*м;  dN_тр = 0.1602;  DN_тр = 0.0002 Н*м

N_тр = 0.0011 ± 0.0002 Н*м;

По   графику:  N_тр = 0,0010 ± 0.0002 Н*м ;  I = 0.0323 Н*м*с²

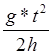I = M*r²*( - 1);   dI = ;   DI = dI*I;

<I> = 0.0220 Н*м*с²;  <DI> = 0.0023 Н*м*с² ;  I = 0.0220 ± 0.0023 Н*м*с²

По  графику:  <I> = 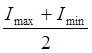 =  0.023 Н*м*с² ;  DI = 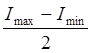 = 0.009 Н*м*с²

I = 0.023 ± 0.009 Н*м*с²;

I₀ = m*l²/12 + m*(P1² + P2²)/4;   I(0) = I_кр + 4I₀;   I = I(0) + 4mR²;

По  графику:  I(0) = 0.0037 Н*м*с²

Вывод: 

1)  Проверяя  справедливость  основного  уравнения  вращательного  движения  Ib = N – N_тр ,     мы  построили  график  зависимости b  от  N  и  получили  прямолинейную  зависимость,  тем  самым  качественно  доказав  справедливость  исходного  уравнения.     График  выходит  из    точки  b = 0   N = N_тр  и    значение  N_тр  по  графику(N_тр = 0,0010 ± 0,0002 Н*м)а измеренное  значение:  N_тр = 0,0011 ± 0,0002 Н*м ;  они  оказались  приблизительно  равны,  что  количественно  доказывает  справедливость  Ib = N – N_тр ;  По  графику  I = 0.0323 Н*м*с²    

2) Проверяя  теорему  Штайнера,  мы  построили  график  зависимости  I = f(R²).  Мы  получили  прямую,  выходящую  из  точки  R = 0  I = I(0),  что  подтверждает  теорему  Штейнера  I = I(0) + 4mR².  Сравнивая  I(0) = 0.0037 Н*м*с²,  I_кр = 0.0032 Н*м*с²  и  I(0) = I_кр + 4I₀ = 0.0035 Н*м*с²  можно  утверждать,  что  теорема  Штайнера  верна.