













ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 1
по курсу “Моделирование систем”
1. Способы получения случайных величин.
2. Марковские системы массового обслуживания. В кабинете флюорографии работает 1 медсестра. Поток пациентов - простейший с параметром l=1/6 человека в мин. В среднем медсестра затрачивает 5 мин на обслуживание одного пациента. Найти пространственно-временные характеристики очереди.
3. Метод
статистического моделирования. Вычислить интеграл методом Монте-Карло 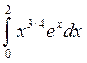 .
.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 2
по курсу “Моделирование систем”
1. Простейший поток
2. Моделирование
дискретных случайных величин. Смоделировать случайную величину ξ, заданную рядом
распределения (параметр с найти): ξ : 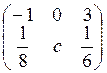 .
.
3. Открытые и замкнутые СМО. Администратор обслуживает дисплейный класс с 12 машинами. Каждая машина выдает требования на обслуживание с интенсивностью 3 машины в день. Среднее время обслуживания – 2 часа. Все потоки – простейшие. Найти среднее число работоспособных машин в течение дня.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 3
по курсу “Моделирование систем”
1. Стохастические системы и возможности их компьютерного моделирования.
2. Оценка точности
и достоверности результатов моделирования. Вычислить интеграл методом
Монте-Карло 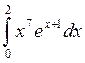 .
.
3. Стационарный пуассоновский поток.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 4
по курсу “Моделирование систем”
1. Метод отбора. Смоделировать случайную величину ξ, равномерно распределенную в секторе, равном четверти круга с радиусом R.
2. Понятие системы массового обслуживания. В магазине "Лига" поток покупателей - простейший с параметром l=1/5 человека в мин. Поток обслуживания – также простейший со средним временем 8 мин. В магазине работают 2 продавца-консультанта. Проверить условие существования стационарного режима.
3. Виды моделирования.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 5
по курсу “Моделирование систем”
1. Понятие системы.
2. Преобразования
случайных величин. Смоделировать случайную величину ξ с заданной функцией
распределения 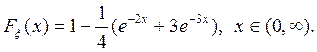
3. Показатели эффективности СМО. Имеется станция связи с двумя каналами. Поток заявок – простейший с параметром l=20 заявок в час. Среднее время обслуживания одной заявки – 4 мин. Найти финальные вероятности состояний и характеристики эффективности СМО.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 6
по курсу “Моделирование систем”
1. Моделирование непрерывных случайных величин (метод обратных функций). Смоделировать случайную величину ξ, равномерно распределенную на интервале
(-2; 5).
2. В среднем пятая часть поступающих в продажу автомобилей некомплектна. Смоделировать случайную величину ξ – число некомплектных автомобилей среди семи автомобилей.
3. Схема рождения и гибели. Открытые и замкнутые системы.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 7
по курсу “Моделирование систем”
1. Классификация систем массового обслуживания
2. Построить
оптимальный алгоритм моделирования сл.в. ξ : 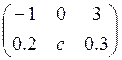 .
.
3. Имеется одноканальная СМО с бесконечной очередью, в которой поток заявок - простейший с параметром l=2 заявок в мин. Среднее время обслуживания одной заявки – 3 мин, среднеквадратическое отклонение – 1 мин. Найти среднюю длину очереди и среднее время пребывания заявки в системе.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 8
по курсу “Моделирование систем”
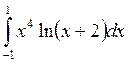 .
.ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 9
по курсу “Моделирование систем”
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 10
по курсу “Моделирование систем”
1. Аналитические и имитационные модели.
2. Немарковские системы. Средняя длина очереди в одноканальных системах.
3. Метод
существенной выборки.
Вычислить интеграл методом Монте-Карло 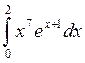 .
.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 11
по курсу “Моделирование систем”
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 12
по курсу “Моделирование систем”
1. Схема гибели и размножения.
2. Статистическая обработка результатов в процессе моделирования систем на ЭВМ.
3.
Оценить
интеграл методом Монте-Карло 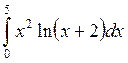 .
.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 13
по курсу “Моделирование систем”
1. Последовательность разработки и компьютерной реализации моделей систем.
2. Формула Литтла. На АЗС 1 колонка, отпускающая бензин одного вида. Поток автомобилей – простейший с параметром l=10 автомобилей в час. Среднее время обслуживания – 5 мин. Найти среднюю длину очереди и среднее время ожидания.
3. Понятие потока.
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 14
по курсу “Моделирование систем”
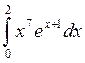 .
.ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 15
по курсу “Моделирование систем”
ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 16
по курсу “Моделирование систем”
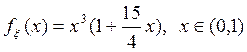 .
.ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 17
по курсу “Моделирование систем”
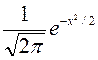 x
xОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 18
по курсу “Моделирование систем”
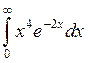 .
.ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ
Кафедра АСУ
Экзаменационный билет № 19
по курсу “Моделирование систем”
1. Использование моделирования при исследовании и проектировании АСОИУ и их элементов
2. Смоделировать последовательность независимых испытаний, в каждом
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.