Аппроксимация таблично заданной функции одной переменной методом наименьших квадратов. Исследование числовых рядов. Решение задач линейного программирования средствами пакета MathCAD

Расчётно-графическое задание

1.  Аппроксимация таблично заданной функции одной переменной методом наименьших квадратов

Пусть некоторая функция задана таблицей своих значений в виде набора чисел  и требуется построить аппроксимирующую функцию вида

, где mn. Метод построения аппроксимирующей функции , при котором величина 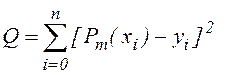минимальна, называется методом наименьших квадратов.

Неизвестные коэффициенты  могут быть найдены из решения системы m+1линейного алгебраического уравнения с m+1 неизвестными вида

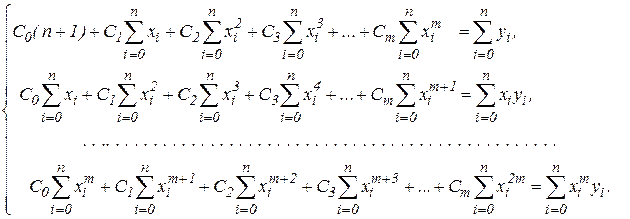
В матричном виде эта система имеет вид  где  - вектор коэффициентов ; Y - вектор значений функции . Матрица , имеющая m+1 столбцов, называется матрицей Вандермонда .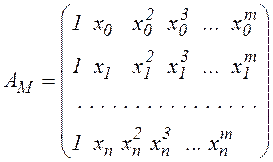

Искомый вектор  находится из матричного уравнения .

Транспонированием называют операцию, переводящую матрицу размерности  в матрицу размерности , делая столбцы исходной матрицы строками, а строки - столбцами. Для этого надо использовать символ транспонирования (третий слева во второй строке) - см. палитру матричных операций, показанную на рис. 1.1. То же самое реализуется комбинацией клавиш Ctrl+1 - как показано на рис.1.2.

Рис. 1.1. Палитра матричных операций

Рис. 1.2. Порядок выполнения матричных операций

Задание.

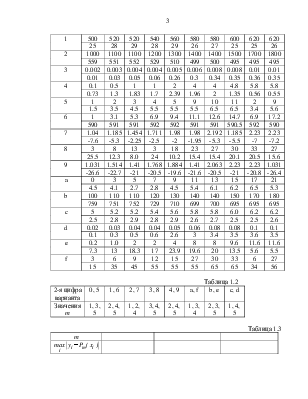
1.1. В соответствии с вариантом задания (см. таблицы 1.1 и 1.2) разработать в среде Mathcad 2000 код программы, вычисляющей коэффициенты  аппроксимирующих функций вида

 по методу наименьших квадратов.

На одной координатной плоскости построить для различных значений m графики этих функций.

Разработать в среде Mathcad 2000 код программы и заполнить таблицу 1.3 для заданных значений m.

Таблица 1.1

Таблица 1.2

Таблица 1.3

2. Исследование числовых рядов

Пусть , , , …, , …, где  − бесконечная числовая последовательность . Выражение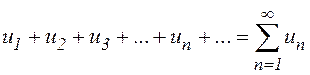

называют бесконечным числовым рядом, а числа , , , …, , … − членами ряда;  называется общим членом. Сумма n первых членов называется n-ой частичной суммой ряда .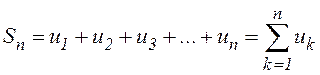

Ряд 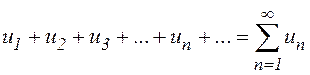 называется сходящимся, если его n-ая частичная сумма при неограниченном возрастании n стремится к конечному пределу, т. е. если . Число S называют суммой ряда. Если n-ая частичная сумма ряда при  не стремится к конечному пределу, то ряд называется расходящимся.

Справедливо следующее утверждение (необходимый признак сходимости ряда). Для того чтобы ряд 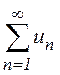 сходился, необходимо, чтобы последовательность его членов  стремилась к нулю при , т. е. . Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом расходится.

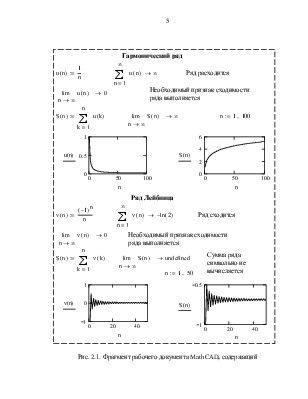
На рис. 2.1 приведён фрагмент рабочего документа MathCAD,содержащий исследование расходящегося и сходящегося рядов; для каждого исследуемого ряда построен график последовательности частичных сумм и членов ряда.

Указание. Для того чтобы вычислить символьно сумму ряда  или предел  в панели , следует щёлкнуть по кнопке  в панели  и по рабочему документу вне выделяющей рамки.

Перечислим важнейшие признаки сходимости и расходимости рядов с положительными членами.

Рис. 2.1. Фрагмент рабочего документа MathCAD, содержащий

исследование расходящегося и сходящегося рядов

1.  Первый признак сравнения. Рассмотрим два числовых ряда с неотрицательными членам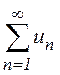и и 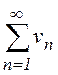, , . Если для всех n, начиная с некоторого, справедливо неравенство , то из сходимости ряда 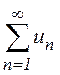 следует сходимость ряда 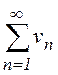; и наоборот, из расходимости ряда  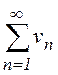следует расходимость ряда .

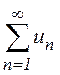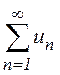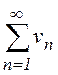2.  Второй признак сравнения. Рассмотрим два числовых ряда с неотрицательными членами и , , . Если 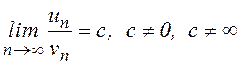, то ряды  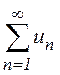и 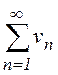 сходятся или расходятся одновременно.

При использовании теорем сравнения исследуемый ряд чаще всего сравнивают с простейшими рядами − с обобщённым гармоническим рядом (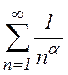, который сходится при  и расходится при ) или с рядом типа прогрессии (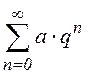,который сходится при  и расходится при ).

На рис. 2.2 приведён фрагмент рабочего документа MathCAD,содержащий исследования сходимости рядов на основе теорем сравнения.

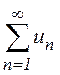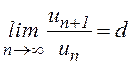3. Признак сходимости Даламбера. Для ряда с положительными членами  ,  , вычислим предел . Если , то ряд 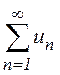 сходится, если  − расходится. При  вопрос о сходимости ряда остаётся открытым: ряд может оказаться как сходящимся, так и расходящимся.

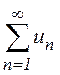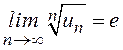4. Признак сходимости Коши. Для ряда с положительными членами  ,  , вычислим предел . Если , то ряд 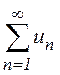 сходится, если  − расходится. При  вопрос о сходимости ряда остаётся открытым: ряд может оказаться как сходящимся, так и расходящимся.

Рис. 2.2. Исследование сходимости рядов на основе теорем сравнения

На рис. 2.3 приведён фрагмент рабочего документа MathCAD, содержащий исследования сходимости рядов с использованием признаков сходимости Даламбера и Коши.

Рис. 2.3. Исследование сходимости рядов на основе признаков

сравнения Даламбера и Коши

Задание

2.1. Выяснить, выполняется ли необходимый признак сходимости рядов. Вычислить сумму ряда. Построить (по возможности) графики для величин членов ряда и его n-ой частичной суммы (). Вариант взять из таблицы  2.1.

2.2. Исследовать сходимость ряда, используя один из признаков сходимости. Построить (по возможности) графики для величин членов ряда и его n-ой частичной суммы (). Вариант взять из таблицы  2.2.

Таблица 2.1

Таблица 2.2

3. Решение задач линейного программирования

средствами пакета MathCAD

Задача поиска условного экстремума функции многих переменных часто встречаются в экономических расчётах для минимизации затрат, максимализации прибыли и т. п. При этом экономическая задача описывается системами линейных уравнений и неравенств и относится к задачам линейного программирования. Типичным примером является так называемая транспортная задача, которая решает проблему оптимальной доставки товара потребителям с точки зрения экономии (минимизации) транспортных расходов.

Пусть у нас имеется N предприятий-изготовителей, производящих