Векторы и операции с ними. Декартова система координат. Базисные векторы и координаты. Теорема о линейной зависимости двух векторов. Теорема о линейной зависимости четырех векторов. Условие принадлежности двух прямых одной плоскости

определяет плоскость, проходящую через начало координат (поскольку координаты начала удовлетворяют этому уравнению).

2)А = 0, уравнение By+Cz + D = 0 определяет плоскость, параллельную оси Ох (поскольку нормальный вектор этой плоскости n = {0, В, C} перпендикулярен оси Ох).

3)В = 0, уравнение Ax+Cz + D = 0 определяет плоскость, параллельную оси Оу (ибо этой оси перпендикулярен нормальный вектор n = {А, 0, C).

4)С=0, уравнение Ах + By + D = 0 определяет плоскость, параллельную оси Oz(ибо этой оси перпендикулярен нормальный вектор n = {А, В, 0}).

5)А = 0, В = 0, уравнение Cz + D = 0 определяет плоскость, параллельную координатной плоскости Оху (ибо эта плоскость параллельна осям Ох и Оу).

6)А = 0, С=0, уравнение By+D = 0 определяет плоскость, параллельную координатной плоскости Охz (ибо эта плоскость параллельна осям Ох и Oz).

7)В = 0, С=0, уравнение Ax+D = 0 определяет плоскость, параллельную координатной плоскости Oyz(ибо эта плоскость параллельна осям Оу и Oz).

8)A = 0, В = 0, D = 0, уравнение Cz = 0 определяет координатную плоскость Оху (ибо плоскость параллельна Оху и проходит через начало координат).

9)A = 0, С=0, D = 0, уравнение Ву = 0 определяет координатную плоскость Oxz (ибо плоскость параллельна Oxzи проходит через начало координат).

10)В = 0, С=0, D = 0, уравнение Ах = 0 определяет координатную плоскость Oyz(ибо плоскость параллельна Оуz и проходит через начало координат).

20.Угол между двумя плоскостями. Условие перпендикулярности и параллельности плоскостей.

Пусть две плоскости П₁, и П₂ заданы общими уравнениями А₁х+ В₁у + С₁z + D₁ = 0 и А₂х + В₂у + C₂z + D₂ = 0. Очевидно, вопрос об определении угла между указанными плоскостями сводится- к определению угла ф между и нормальными векторами n₁ ={А₁ В₁ С₁) и n₂ = {А₂, В₂, С₂ }.

Из определения скалярного произведения n₁n₂ = | n₁| |n₂| cos ф и из выражения в координатах длин векторов n₁, и n₂ и их скалярного произведения, получим

Условие параллельности плоскостей П₁, и П₂, эквивалентное условию коллинеарности векторов n₁, и n₂, заключается в пропорциональности координат этих векторов, т.е. имеет вид

Условие перпендикулярности плоскостей П₁ и П₂ может быть извлечено из формулы при cosф = 0) или выражено равенством нулю скалярного произведения векторов n₁, и n₂. Оно имеет вид 

A_lA₂ + B₁B₂+C₁C₂ = 0.

21.Нормальное уравнение плоскости. Отклонение точки от плоскости.

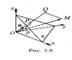Рассмотрим какую угодно плоскость П. Проведем через начало координат О прямую п, перпендикулярную плоскости л, и обозначим буквой Р точку пересечения прямой п и плоскости тс (рис. 5.9). На прямой я возьмем единичный вектор n, направление которого совпадает с направлением отрезка ОР (в случае совпадения точек О и Р направление n выберем произвольно).

Поставим перед собой цель — выразить уравнение плоскости П через следующие параметры: 1) длину р отрезка ОР; 2) утлы а, b и у наклона вектора n к осям