Последовательная интерполяция (геометрическая интерполяция функции 2-х переменных). Формула Лагранжа для неравностоящих узлов. Способы организации размещения и поиска информации в ЭВМ. ВЗУ на магнитных дисках

Вопрос 1

Интерполяция функций многих (2-х) переменных

Пусть на плоскости XY задана таблично n+1 точка (узлы интерполяции):

x₁ x₂…x_n

y₁ y₂…y_n

f(x₁,y₁)        (x₂,y₂)…f(x_n,y_n)

Будем искать интерполирующую функцию F_m(x,y)=C₀₀+C₁₀x+C₀₁y+C₂₀x²+C₁₁xy+C₀₂y²+…+C_m0x^m+C_m-1x^m-1y+C_m-2x^m-2y²+…+C_0my^m.

Когда имеется (n+1) точка в исходных данных, например:

x₀ x₁ …x_n

y₀  y₁ …y_n

f(x₀,y₀) f(x₁,y₁)…f(x_n,y_n), то можем для решения задач интерполяции (т.е. нахождения C_ij ,  ) составить СЛАУ из (n+1) уравнения:

C₀₀+C₁₀x₀+C₀₁y₀+ …+C_m0x₀^m+…+C_0my₀^m==f(x₀,y₀),

C₀₀+C₁₀x₁+C₀₁y₁+ …+C_m0x₁^m+…+C_0my₁^m==f(x₁,y₁),

…

C₀₀+C₁₀x_n+C₀₁y_n+ …+C_m0x_n^m+…+C_0my_n^m==f(x_n,y_n).

Очевидно, n+1 должно равняться 1+2+3+…+(m+1)=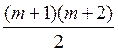. Это первое принципиальное отличие интерполяции функции 2-х (многих) переменных от интерполяции функции одной переменной – не можем произвольно выбирать число узлов интерполяции. Если последнее тождество не выполняется, то часть из коэффициентов C_ij приходится занулять, причем нет разумных рекомендаций, какую именно.

Вопрос 2

Формула Лагранжа для неравностоящих узлов.

В практике вычислений часто требуется определить значение функции f(x), определенной своими значениями f(x₀), f(x₁), …, f(x_n) на определенном наборе точек (узлов) , в некоторой промежуточной точке , где i=0, 1, … , n-1. Построение функции F(x), позволяющей вычислить значение функции f(x)в точках, не совпадающих с заданным набором узлов, называется задачей интерполяции функции одной переменной. При этом f(x) называют интерполируемой, а F(x) – интерполирующей функциями. Определение значения функции f(x) для x<a или x>b, называется задачей экстраполяции. При решении этих двух задач часто используются интерполяционная формула Лагранжа для неравноотстоящих узлов, приведенная ниже

.

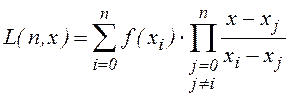Вопрос 5

Последовательная интерполяция (геометрическая интерполяция функции 2-х переменных)

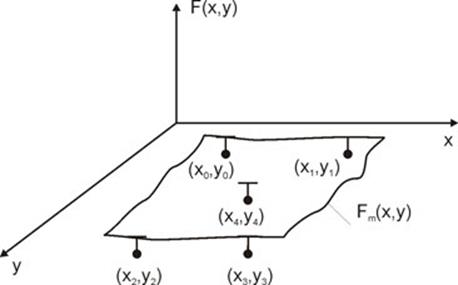
F_m(x,y) – уравнение поверхности.

Трудность: не можем произвольно на плоскости XY располагать узлы интерполяции.

Для F₁(x,y) узлы интерполяции не должны лежать на одной прямой линии.

C₀₀+C₁₀x₀+C₀₁y₀=f(x₀,y₀),

C₀₀+C₁₀x₁+C₀₁y₁=f(x₁,y₁),

C₀₀+C₁₀x₂+C₀₁y₂=f(x₂,y₂).

.

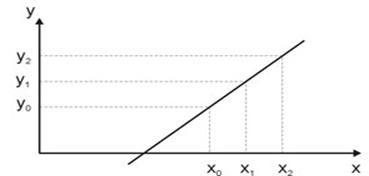
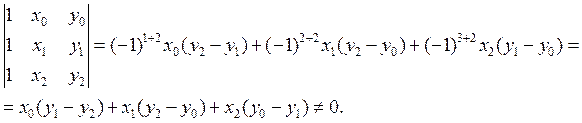
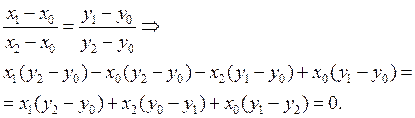
- это уравнение прямой линии.

Аналогично, при m=2 узлы интерполяции не должны располагаться в плоскости XY на линии 2-го порядка и.т.д., т.е. перед выполнением интерполяции функции 2-х (многих) переменных следует вычислить .

Трудности значительно ограничивают область применения интерполяции функции многих переменных.

Обычно ограничиваются значениями m=1, 2.

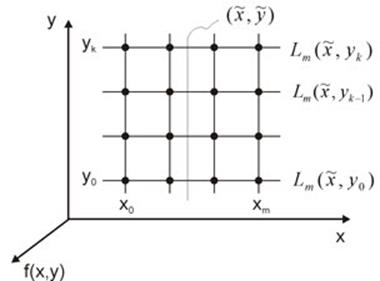
Пусть на плоскости XY задана сетка:

При этом желательно, чтобы сетка была равномерной. Необходимо найти значения .

Последовательная интерполяция состоит из 2-х этапов:

1) для каждого из (k+1)-го набора узлов интерполяции выполняют интерполяцию для фиксированных значений y, например, используя формулу Ларанжа для функции одной переменной;2) один раз для найденных значений L_m (всего k+1) вычисляют

Вопрос 6

Аппроксимация функции одной переменной

Пусть на плоскости XY таблично определена функция 1-й переменной:

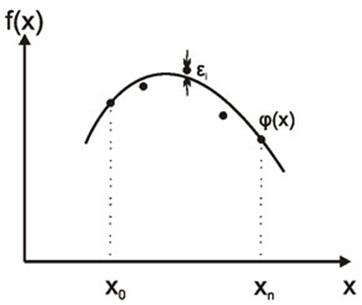Задача нахождения функции φ(x), которая бы отражала заданную функцию f(x), необязательно совпадая с её значением в узлах аппроксимации, называется задачей аппроксимации.

φ(x) может совпадать со значением f(x).

Ограничимся рассмотрением функции φ(x) вида φ_m(x)=C₀+C₁x+C₂x²+…+C_mx^m, где, как правило, m<<n. Если m=n, то имеем задачу интерполяции.

Метод, в котором величина 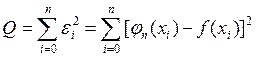 минимальна, называется методом наименьших квадратов (самый распространенный метод).

В соответствии с мат.анализом Q минимальна, если .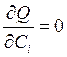

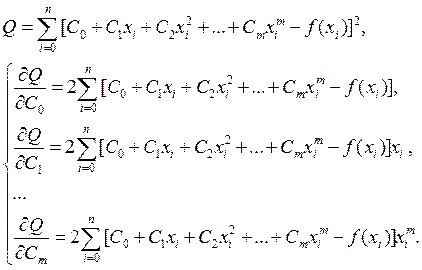
Имеем СЛАУ из (m+1)-го уравнения.

Решив её, найдем искомые C_i. Эту систему удобно переписать в другом виде:

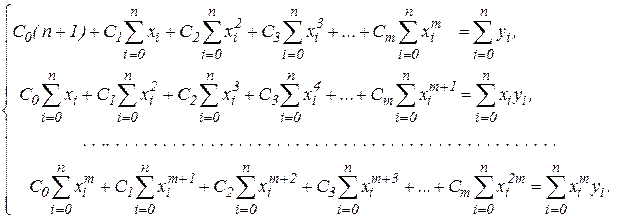
Вопрос 7

Явление волнистости и сплайны

Пусть таблично задана f(x):

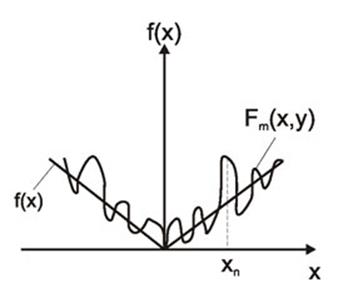
Достаточно часто при выполнении интерполяции или аппроксимации степенным полиномом наблюдается следующее явление.

Пусть

F_m(x)=C₀+C₁x+C₂x²+…+C_mx^m, m≤n.

Значение F_m(x) между узлами может сколь угодно сильно отличаться от f(x) в близлежащих узлах.

С ростом m значение F_m(x) не приближается к f(x).

Явление осцилляции – фундаментальное свойство полиномов и проявляется обычно при m≥5.

Для борьбы с этим явлением используют кусочнополиномиальную интерполяцию или аппроксимацию. Два соседних узла при этом соединяются куском линии 2-го или 3-го порядков.

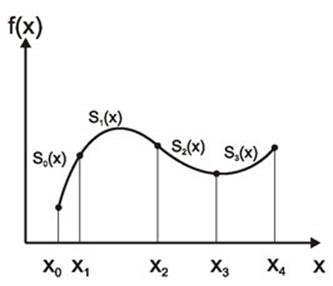
S(x) называется сплайном порядка p, определенным на множестве узлов, если:

1) на каждом из частичных подотрезков

[x_i,x_i+1],

S(x)=S_i(x)=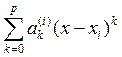

или

S(x)=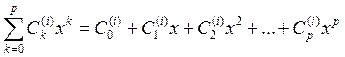, p≤3;