Математика \ Численные методы

Последовательная интерполяция (геометрическая интерполяция функции 2-х переменных). Формула Лагранжа для неравностоящих узлов. Способы организации размещения и поиска информации в ЭВМ. ВЗУ на магнитных дисках, страница 2

2) S(x)Cp-1 [a,b], a=x0, b=xn, т.е. S(x) (p-1)-раз дифференцируемая на [a,b].

Очевидно, необходимо определить n(p+1) коэффициентов .

Из 2-го условия следует, что в (n-1)-м промежуточном узле должны выполняться условия:

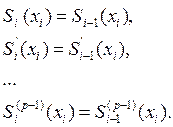
Итого p уравнений в узле. Всего имеем (n-1)p уравнений.

Остается определить n(p+1)-(n-1)p=n+p коэффициентов.

При решении задачи интерполирования для всех узлов должно выполняться S(xi)=f(xi) – (n+1) уравнение.

Тогда неопределенными останутся n+p-(n+1)=p-1 коэффициент. Как правило, недостающие p-1 уравнение получают при интерполяции, принудительно задавая S’(x0) и, если необходимо, S’(xn).

При выполнении аппроксимации недостающие (n+p) уравнения получаем, используя те или иные методы приближения Fm(x) к f(x), например, метод наименьших квадратов.


Вопрос 8

Численные методы решения систем нелинейных уравнений

Системой из n нелинейных уравнений с n неизвестных называется выражение вида

f1(x1,x2,…,xn)=0,

f2(x1,x2,…,xn)=0,

…

fn(x1,x2,…,xn)=0, где fi(x1,x2,…,xn)=0 – некоторое уравнение от n-переменных.

Решением СНУ является всякий вектор (x1,…xn) или набор числе x1,…xn, который обращает систему в тождество.

У СНУ решений, как правило, множество.

В матричной форме система запишется в виде

, где , .

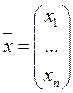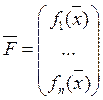Решение СЛАУ и СНУ – вектор.

Метод простой итерации:

Исходную СНУ всегда можно переписать в виде:

x1=φ1(x1,x2,…,xn),

x2=φ2(x1,x2,…,xn),

…

xn=φn(x1,x2,…,xn).

Обозначив

,

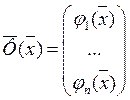Можем записать:


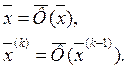
Вопрос 9

Численные методы решения ОДУ

ДУ n-го порядка называется выражение φ(x,y,y’,y’’,…,y(n))=0. Решением ДУ является вякая функция y(x), которая обращает ДУ в тождество.

Численные методы решения ДУ используют, если не удается найти аналитическое решение (т.е. записанное в известных элементарных функциях), или когда функция задана поточечно. Приближенное решение бывает удобнее аналитического.

Все численные методы решения ДУ делятся на 2 группы: 1) решение получается в виде приближенного аналитического выражения в известных функциях; 2) решение получается в виде табличных значений x0, y0, x1, y1…


Вопрос 10

Метод Эйлера решения ОДУ первого порядка

ОДУ 1-го порядка имеет вид:

.

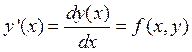В той постановке, что мы рассмотрели выше, ОДУ имеет бесчисленное множество решений. Необходимо наложить ограничения на решение.

Поиск решения ОДУ, при котором требуется, чтобы y(x) и её первые (n-1) производная проходили бы через заданную точку, называется задачей Коши.

y0=y(x0), y10=y’(x0),…, yn-10=y(n-1)(x0).

Пусть надо найти y(x): разложим по Тейлору y(x) в окрестности точки x0.

.

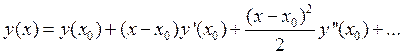Ограничимся первыми тремя членами разложения:

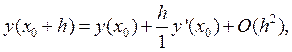
h=x-x0, где O(h2) – величина бесконечно малая порядка h2.

x0+h=x1.

y(x1)≈y(x0)+hy’(x0),

y(x2)≈y(x1)+hy’(x1),

…

y(xi)≈y(xi-1)+hy’(xi-1).

Таким образом, y’(xi-1)=f(xi-1,yi-1).

В общем случае погрешность оценивается формулой Рунге:

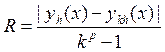, где yh(x) – приближенное решение при шаге h, k – некоторое целое число (обычно 2), ykh(x) - решение ОДУ при шаге k*h, p – глобальный порядок точности. Для метода Эйлера p=1. Она определяется максимальной степенью производной, принятой во внимание при разложении y(x) в ряд Тейлора.


Скачать файл