Ответы на экзаменационные вопросы № 1-17 дисциплины "Численные методы" (Арифметические действия с двоичными числами. Метод Зейделя)

1 Арифметические действия с двоичными числами.

2 Вопросы погрешности в различных позиционных СС.

3 Представление десятичных чисел в D-кодах.

4 Приближенное решение НУ. Постановка задачи.Локализация корней.

5 Уточнение корня методом половинного деления (дихотомии).

6 Уточнение корня методом неподвижных хорд. Алгоритм метода в текстуальной и графической форме.

7 Уточнение корня методом подвижных хорд (секущих). Алгоритм метода в текстуальной и графической форме.

8 Уточнение корня методом касательных (Ньютона). Алгоритм метода в текстуальной и графической форме.

9 Уточнение корня модифицированным методом касательных (Ньютона). Алгоритм метода в текстуальной и графической форме.

10 Уточнение корня методом простой итерации. Алгоритм метода в текстуальной и графической форме.

11 Численные методы линейной алгебры. Постановка задачи.

12 Формула Крамера.

13 Вычисление определителя.

14 Метод Гаусса.

15 Критерий завершения вычислений для итерационных методов.

16 Метод итераций решения СЛАУ.

17 Метод Зейделя.

Вопрос 1 ОПЕРАЦИИ С 2-МИ ЧИСЛАМИ

Сложение:

Нужно знать таблицу сложения: 0+0=0, 1+0=0+1=1, 1+1=10.

Сложение выполняется схоже с 10сс. Если в складываемых разрядах расположены «1», то в соответствующем разряде устанавливают «0»

и единицу переводят в старший разряд.

Вычитание:

Нужно знать таблицу вычитания: 0-0=0, 1-0=1, 1-1=0, 10-1=1.

Вычитание выполняется схоже с 10сс. Если в уменьшаемом разряде расположен «0», а в вычитаемом «1», то в соответствующем разряде разности устанавливают «1» и выполняют заем из старшего разряда.

Умножение:

Выполняется аналогично 10сс, но частичными произведениями могут быть либо множимое, либо 0.

В 2сс умножение сводится к сдвигу множимого и сложения.

Деление:

Производится подобно 10сс. При делении смешанных чисел количество знаков в дробной части уравнивается путем добавления нулей.

Вопрос 2   ВОПРОСЫ ПОГРЕШНОСТИ ПРИ ПЕРЕВОДЕ СС

Пусть .

- для хранения выделяется np разрядов.

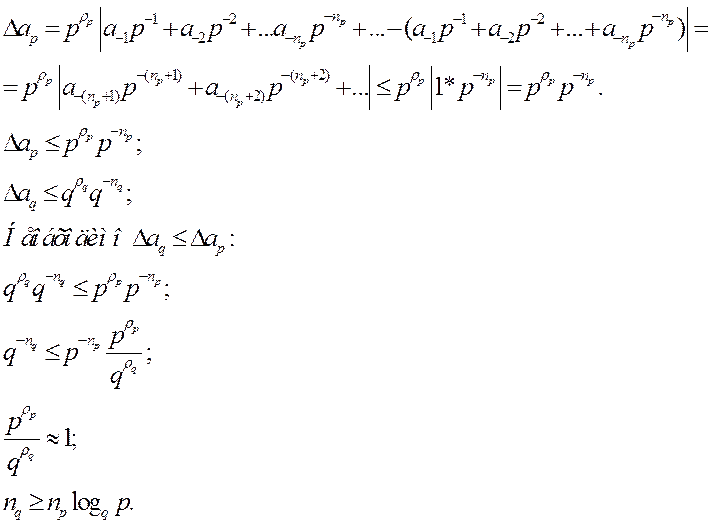
Вопрос 3      Представление десятичных чисел в Д-кодах

Д-код – такое представление 10-чного числа, при котором его разряды записываются с помощью двоичных цифр.

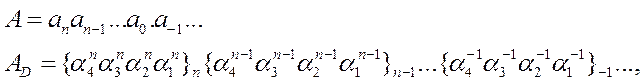
где - двоичные числа.

Для однозначного преобразования представления числа в

Д-код необходимо разрядам тетрады придать вес.

Тогда

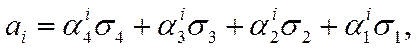
где , , ,  - веса разрядов.

Нашли распространение следующие Д-коды:

Десятичная цифра	Наименование Д-кода
	8421	8421+3	2421
0	0000	0011	0000
1	0001	0100	0001
2	0010	0101	0010
3	0011	0110	0011
4	0100	1111	0100
5	0101	1000	1011
6	0110	1001	1100
7	0111	1010	1101
8	1000	1011	1110
9	1001	1100	1111

При составлении Д-кода следует придерживаться следующих правил:

1) разным десятичным числам должны соответствовать разное Д-кодирование;

2) большей десятичной цифре должен соответствовать больший Д-код;

3) если 2 десятичные цифры A и B представлены в Д-коде и связаны соотношением A+B=9, то

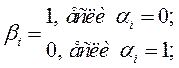
Вопрос 4 – РЕШЕНИЕ НУ

Нелинейным алгебраическим уравнением называется выражение вида

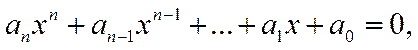
где целые числа.

Нелинейное уравнение, которое не является алгебраическим, называется трансцендентным.

Решением НУ является всякое значение x, которое обращает

НУ в верное тождество.

Численное решение НУ разбивается на 2 этапа:

а) локализация (отделение) корней – нахождение участков по оси x, где корень существует и единственен;

б) уточнение положения корня до необходимой точности.

2. Локализация корней

Теорема:

Пусть f(x) из уравнения f(x)=0 непрерывна на [a,b], кроме того,

f(a)*f(b)<0, следовательно,

.

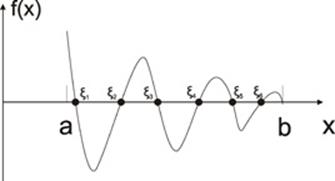
Если , которая знакопостоянна, то  - единственный корень:

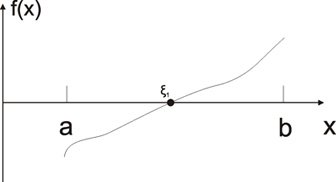
Для ЭВМ:

а) находят знаки функций в концах отрезка;

б) длят отрезок [a,b].

Желательно построить Г(f(x)) и Г(f’(x)).

Вопрос 5 – МЕТОД      ДИХОТОМИИ

Уточнение корня методом половинного деления (дихотомии).

Пусть дано уравнение f(x)=0, где функция f(x) непрерывна на

[a,b] и f(a)*f(b)<0.

Для нахождения корня уравнения, принадлежащего отрезку

[a,b], делим этот отрезок пополам. Если f()=0, то = является корнем уравнения. Если f()≠0, то выбираем ту из половин 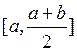 или 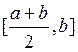, на концах которой функция

f(x) имеет противоположные знаки. Новый суженный отрезок снова делим пополам и проводим рассмотрение заново.

Сходимость метода определяется количеством необходимых вычислений f(x).

Вопрос 6 – МЕТОД      НЕПОДВИЖНЫХ ХОРД

Данный метод схож с методом дихотомии. Отличие состоит в том, что текущий отрезок делится не пополам, а в соотношении 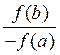, при этом положение точки, делящей отрезок, выражается формулой

.

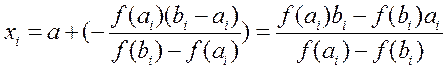Неподвижным у хорды будет конец [a,b], для которого f’’(x)*f(a или b)>0.

Вычисления прекращают, когда |xn-xn-1|<ε.

Метод сходится быстрее метода дихотомии, но необходимо исследовать вторую производную.

Вопрос 7 – МЕТОД      ПОДВИЖНЫХ ХОРД

Метод подвижных хорд (секущих) является обобщением метода неподвижных хорд в том смысле, что конец хорды не закреплен.

Формула, вычисляющая положение очередного приближения к искомому корню, выглядит следующим образом:

.

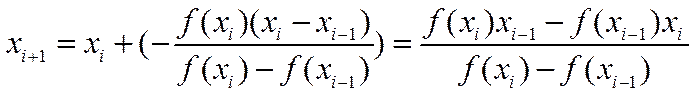Метод сходится, но немонотонно.

Вопрос 8 – МЕТОД      КАСАТЕЛЬНЫХ