Пусть
дано НУ f(x)=0, где ![]() ,
кроме того, f(a)f(b)<0.
,
кроме того, f(a)f(b)<0.
f '(x) и f ’’(x) определены, не равны нулю, непрерывны и знакопостоянны на [a,b].
Пусть корень ξ уравнения отделен на отрезке [a,b]. Найдя какое-нибуд ь n-е приближенное значение корня xn≈ξ (a≤ xn≤b), можем уточнить его по методу Ньютона следующим образом. Положим ξ=xn+hn.
Отсюда, применяя формулу Тейлора, получим:
0=f(xn+hn)≈f(xn)+hnf‘(xn).
Следовательно,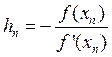 .
.
Внеся эту поправку, найдем следующее приближение корня
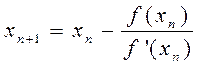 (n=0,1,2,…).
(n=0,1,2,…).
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой.
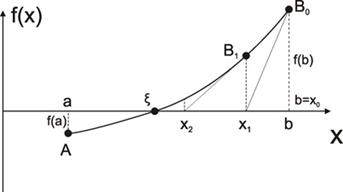
Выберем, например, x0=b, для которого f(x0)f ’’(x0)>0. Уравнение касательной точке Bn[xn,f(xn)] (n=0,1,2,…):
y-f(xn)=f’(xn)(x-xn).
Полагая
y=0, x=xn+1, получим: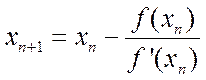 .
.
«Хорошим» начальным приближением x0 является то, для которого выполнено неравенство
f(x0)f ’’(x0)>0.
Достоинства: метод сходится всегда и быстро, если правильно выбрано начальное приближение.
Недостатки: необходимо исследовать поведение второй производной на всем [a,b].
Вопрос 9 – МОДИФИЦ МЕТОД КАСАТЕЛЬНЫХ
Пусть
дано НУ f(x)=0, где ![]() ,
кроме того, f(a)f(b)<0.
,
кроме того, f(a)f(b)<0.
f '(x) и f ’’(x) определены, не равны нулю, непрерывны и знакопостоянны на [a,b].
Если производная f ’(x) мало изменяется на отрезке [a,b], то можно положить:
f ‘(xn)≈f ‘(x0). Тогда очередное приближение к корню выражается формулой
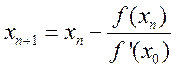 .
.
Геометрически этот способ означает, что мы заменяем касательные в точках Bn[xn,f(xn)] прямыми, параллельными касательной к кривой y=f(x), в её фиксированной точке B0[x0,f(x0)].
По сравнению с методом Ньютона не требуется каждый раз вычислять значение первой производной.
Вопрос 10 – МЕТОД ПРОСТЫХ ИТТЕРАЦИЙ
Пусть f(x)=0, где f(x) непрерывна на [a,b], причем f(a)f(b)<0, а также f ‘(x) непрерывна и знакопостоянна на [a,b], т.е. корень существует и единственный.
Заменим уравнение f(x)=0 уравнением x=φ(x).
Выберем каким-либо образом приближенное значение корня x0 и подставим в правую часть уравнения x=φ(x). Получим новое приближение к корню x1=φ(x0) и.т.д.
|
Графически процесс итерации выглядит следующим образом: |
|
При |φ’(x)|≥1 вероятно, что процесс итерации расходится.
Метод сходится достаточно быстро (сравнимо со скоростью метода Ньютона).
Недостаток: необходимо исследовать поведение функции f ’(x) и φ’(x).
Вопрос 11 – ЧИСЛОВЫЕ МЕТОДЫ ЛИНЕЙ АЛГЕБРЫ
Есть СЛАУ:
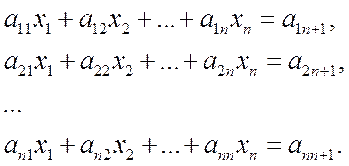
![]() .
.
Решением СЛАУ является всякий набор чисел x1…xn, которые обращают
СЛАУ в верное тождество. СЛАУ может иметь одно или множество решений или не иметь решений.
Интересует случай с единственным решением. В матричной форме СЛАУ
имеет
вид![]() .
.
СЛАУ имеет единственное решение, если определитель основной матрицы
A не равен 0.
Все численные методы делятся на следующие:
1) прямые – решение получается за конечное число действий. Используется
2) при n<200;
3) итерационные – приближение к решению получается за конечное число
4) шагов (n>200).Учитывая ошибку машинной арифметики, не можем
5) получить точное решение даже для прямых методов.
В общем случае оценить погрешность вычисления корня невозможно.
Вопрос 12 - Формула Крамера.
Пусть
дана СЛАУ, причем ![]() .
.
i-я компонента вектора решений вычисляется по формуле
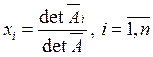
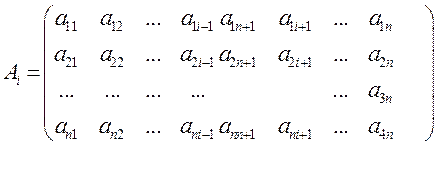
![]() =
=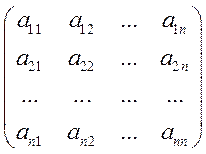 .
.
Вопрос 13 - ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ
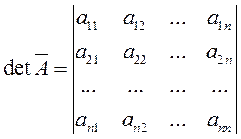 .
.
Пусть
a11![]() . Поделим все элементы
первого столбца на него.
. Поделим все элементы
первого столбца на него.
 .
.
Вычтем
из 2-й, 3-й, n-й строк элементы первой строки, умноженные на 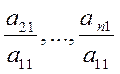 , так чтобы получить нули в первом
столбце.
, так чтобы получить нули в первом
столбце.
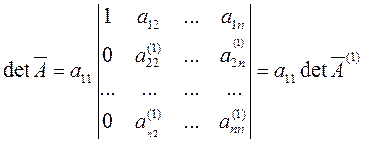 ,
,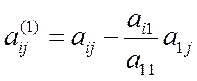
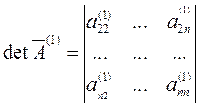
.
На шаге k=2 и.т.д., выполняем аналогичные манипуляции и получаем
![]() .
.
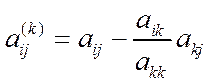 , k≤n-1,
, k≤n-1, ![]() .
.
Для
вычисления определителя n-го порядка необходимо выполнить 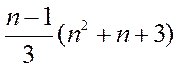 умножений и делений.
умножений и делений.
Вопрос 14 - МЕТОД ГАУССА РЕШЕНИЯ СЛАУ.
Пусть дана СЛАУ.
Расширенная матрица этой системы:
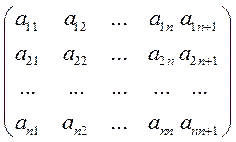 .
.
Будем приводить матрицу к треугольной форме, т.е. когда все элементы ниже главной диагонали равны 0.
Полагая, что a11≠0, поделим все элементы первой строки на него.
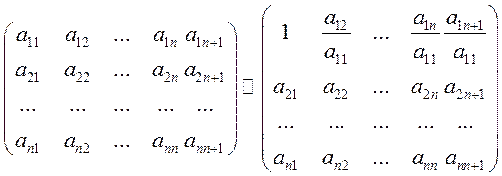
Вычтем из 2-й строки первую, умноженную на a21, из 3-й строки – первую, умноженную на a31 и т.д. В результате получим матрицу:
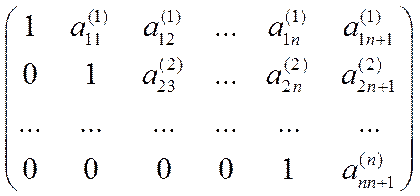 .
.
Если
на k-м шаге вдруг окажется, что ![]() , то выполняют перестановку
строк или столбцов, так чтобы
, то выполняют перестановку
строк или столбцов, так чтобы 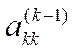 оказался не равным
нулю.
оказался не равным
нулю.
Данная
комбинация действий называется прямым ходом, в результате которого
вычисляется xn=![]() .
.
Оставшиеся компоненты вектора решений находят по формуле:
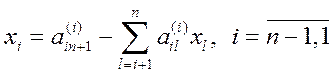 .
.
Для
СЛАУ порядка n необходимо при вычислении корня или решения выполнить
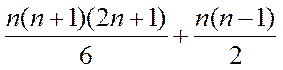 действий.
действий.
Вопрос 15 - Критерий завершения процесса вычислений
Если
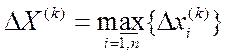 ,
, 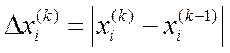 , как
и критерий завершения для методов неподвижных хорд, Ньютона и модиф.
, как
и критерий завершения для методов неподвижных хорд, Ньютона и модиф.
Ньютона решения НУ.
Вопрос 16 - Метод итераций
Данный метод дет приближенные результаты.
Пусть дана СЛАУ:
Ax=b.
Предполагая,
что aii≠0 (![]() ), выразим
x1,…,xn:
), выразим
x1,…,xn:
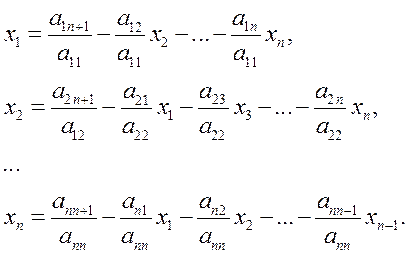
Если akk=0, то можем в СЛАУ переставить строки или столбцы.
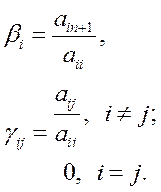
Получим,![]() .В итоге решение СЛАУ сводится
к последовательности шагов:
.В итоге решение СЛАУ сводится
к последовательности шагов:
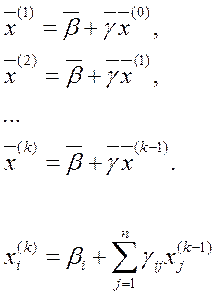 Если неизвестны начальные
приближения, то принимают
Если неизвестны начальные
приближения, то принимают 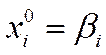 .
.
Вопрос 17 - Метод Зейделя.
Метод Зейделя представляет собой некоторую модификацию метода итераций. Основная его идея заключается в том, что при вычислении
(k+1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k+1)-е приближения неизвестных x1,…,xi-1.
Пусть дана приведенная линейная система
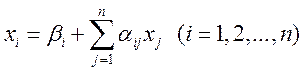 .
.
Выберем произвольно начальные приближения корней
![]() .
.
Далее,
предполагая, что k-е приближение 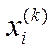 корней известны, согласно
Зейделю будем строить (k+1)-е приближения корней по следующим
формулам:
корней известны, согласно
Зейделю будем строить (k+1)-е приближения корней по следующим
формулам:
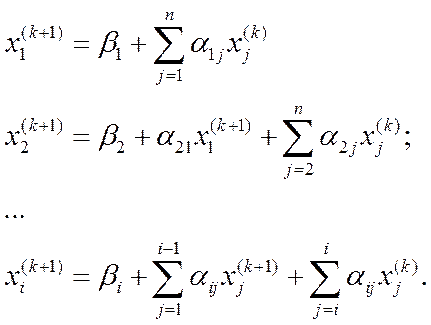
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.