Методические указания к РГЗ
Часть 2
1. Требования
Прежде, чем оформлять пояснительную записку по РГЗ Вы должны продемонстрировать работающую программу преподавателю. Оформленная записка сдается преподавателю на проверку, и после проверки защищается. Пояснительная записка должна содержать:
· титульный лист установленного образца;
· задание;
· схемы алгоритмов всех функций;
· текст программы с комментариями;
· результаты работы программы для разных точностей вычисления;
· выводы.
Небрежно оформленное РГЗ на проверку не принимается!
1. Ваша программа должна состоять из функции main() и четырёх пользовательских функций, которые вы создадите в процессе работы над РГЗ. Это подынтегральная и первообразная функции и функции вычисления интеграла методом Ньютона - Котеса и Гаусса. Первообразная функция нужна вам для проверки правильности вычисления интеграла приближенными методами.
2. Обмен между функциями можно производить только через аппарат формальных/фактических параметров. В качестве глобальной переменной можно использовать только количество обращений к подынтегральной функции.
3. Все применяемые функции, а также их параметры (аргументы) должны иметь тип double.
4. Для сокращения записи целесообразно использовать инструкцию typedef в виде:
5.
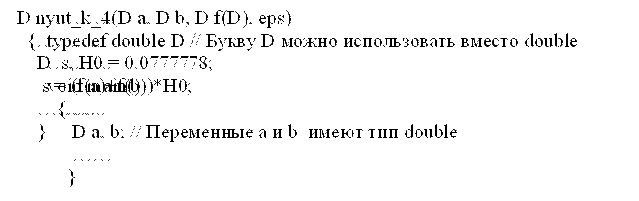 |
Здесь a,b – нижний и верхний пределы интегрирования, f() – подынтегральная функция, eps – заданная точность вычисления интеграла. Обращение к функции nyut_k_4() может иметь вид:
nyut_k_4 (1.2, 2.4, fun, 0.0001);
Естественно, что к моменту обращения к функции nyut_k_4() функция fun() должна быть определена, например, если подынтегральная функция f(x)=sin2 (x), то функция fun() запишется так:
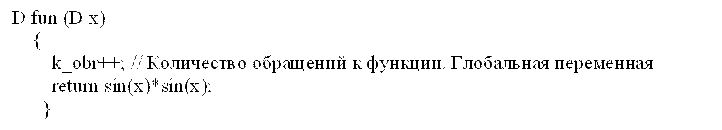 |
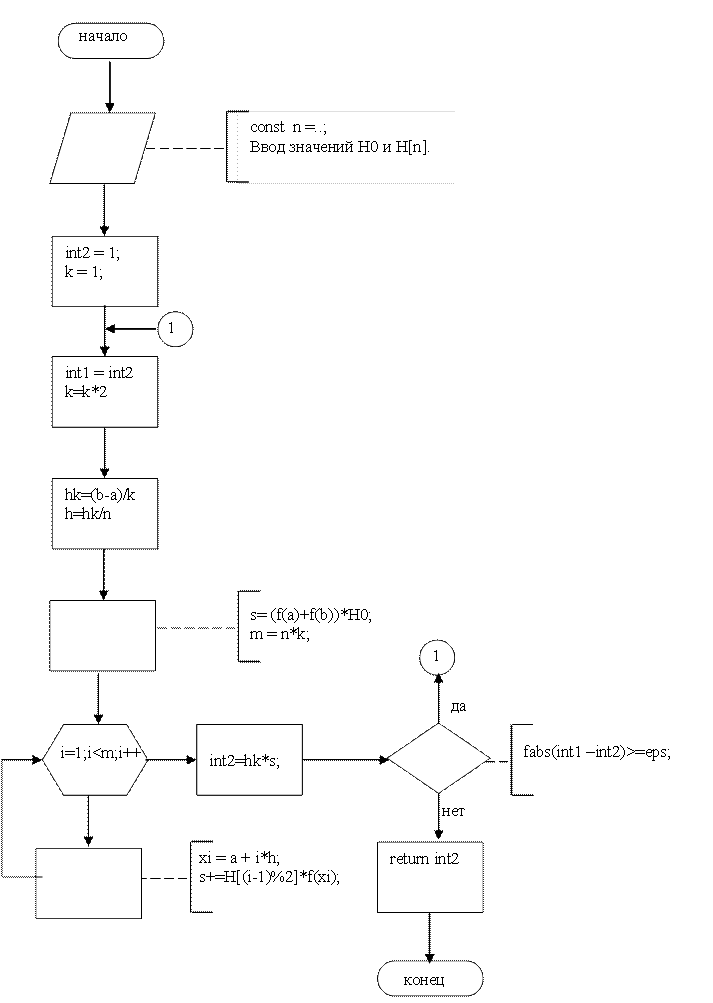
Для вычисления определенных интегралов по формуле Ньютона – Котеса для любых значений n следует промежуток интегрирования [a,b] разделить на k равных частей и для каждой части, применив выбранную (заданную) квадратурную формулу, определить её площадь. После суммирования этих площадей Вы и получите значение интеграла.
Пусть n=2, а k=2, т.е. промежуток интегрирования [a,b] делится на две равные части
 |

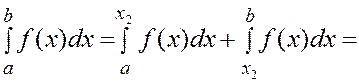 Int.
(1)
Int.
(1)
Применяя к каждому интегралу в правой части (1) квадратурную формулу
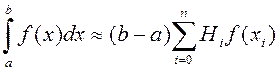 , для n=2,
получим
, для n=2,
получим
Int » 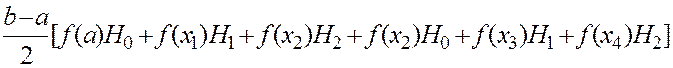
Т.к. Н0=Н2, то
Int»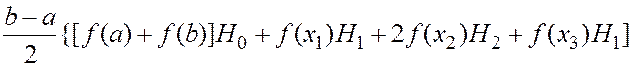
Распространим последнее выражение на случай произвольных n и k
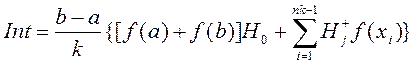 , (2)
, (2)
где
j = 1, 2, …,n, 1, 2,
…n, 1, 2, …;![]() .
.
Для реализации выражения (2) на языке С++ необходимо
набор коэффициентов ![]() (коэффициент H0 в этот набор не
входит! ) оформить в виде массива, не
забывая, что индексы массива начинаются с нуля. Если вычислять индексы
элементов массива Н[j] по формуле j=(i-1)%n ,
то они будут меняться с нужной периодичностью, т.е. 0, 1, 2, …., n-1,
0, 1, 2, ….,n-1, 0… .
(коэффициент H0 в этот набор не
входит! ) оформить в виде массива, не
забывая, что индексы массива начинаются с нуля. Если вычислять индексы
элементов массива Н[j] по формуле j=(i-1)%n ,
то они будут меняться с нужной периодичностью, т.е. 0, 1, 2, …., n-1,
0, 1, 2, ….,n-1, 0… .
Таким образом, при n =2 массив Н[j] примет вид (см. табл.3 методических указаний ):
H[2] = {4./6, 2./6}, H0=1./6 или H[2] = {0.6666667, 0.3333334} и H0=0.1666667 (обратите внимание, что элемент H[1] мы увеличили в два раза!) , а j примет значения 0, 1, 0 (см. рис.1).
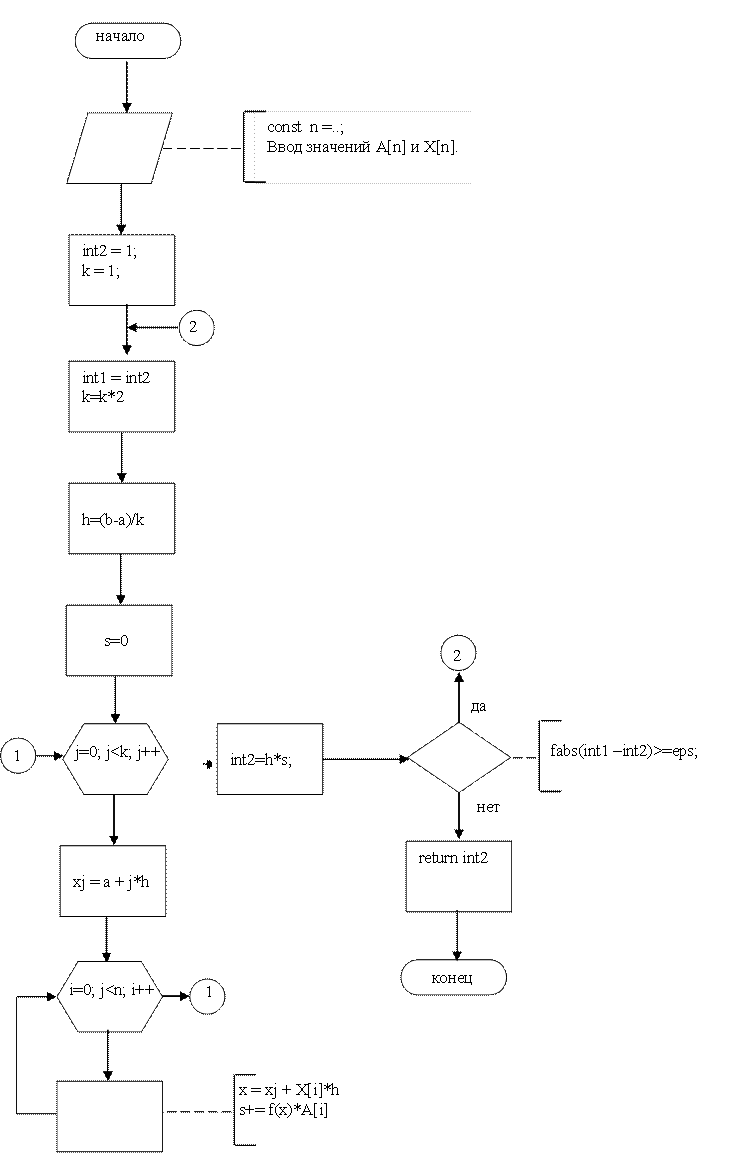
Реализация этого метода на языке С++ не вызывает у студентов особых трудностей. Однако на этапе оформления методических указаний, которыми Вы пользуетесь, в общую формулу Гаусса (14) вкрались опечатки. В тексте, который приведён ниже, они устранены.
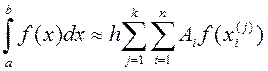 ,
(3)
,
(3)
где h=(b-a)/k – шаг интегрирования;
![]() -
i-ая абсцисса j-ого шага интегрирования: x0 = a, xj=xj-1+h, j=1,2,…,k;
-
i-ая абсцисса j-ого шага интегрирования: x0 = a, xj=xj-1+h, j=1,2,…,k;
![]() =xj-1+Xih , i=1,2,…, n;
=xj-1+Xih , i=1,2,…, n;
Xi, Ai – абсциссы и коэффициенты формулы Гаусса (табл. 4 мет. указаний).
5. Структура программы
Прототипы функций.
Подынтегральная функция
Первообразная функция
Функция вычисления интеграла методом Гаусса для n = 4
Функция вычисления интеграла методом Ньютона-Котеса для n = 4
voidmain ()
{
Описание типов переменных, открытие файла для добавления (запись в конец файла).
Вычисление интеграла через первообразную (точное значение интеграла).
Введение с клавиатуры требуемой точности вычисления интеграла.
Вычисление интеграла методом Гаусса при n = 4
Обнуление количества обращений к подынтегральной функции
Вычисление интеграла методом Ньютона - Котеса при n = 4.
Вывод результатов на экран и запись в файл.
}
Определение всех функций (их содержание).
6. Примеры прототипов используемых функций
typedef double D; // Даёт типу данныхdouble новое имя D.
long int kf; // kf – к-во обращений к подынтегральной функции (глобальная переменная)
D fun(D x); // Подынтегральная функция. Одним из операторов этой функции будет kf++;
D perv_obr(D x); // Первообразная функция
// Функция вычисление интеграла методом Гаусса для n=4
D gauss_4(D a, D b, D f(D), D eps);
// Функция вычисление интеграла методом Ньютона-Котеса для n=4
D nyut_k_4( D a, D b,D f(D), D eps);
Здесь x – аргумент подынтегральной функции a,b – нижний и верхний пределы интегрирования,f()- подынтегральная функция, eps – точность вычисления интеграла. Это формальные параметры. При обращении к функции (её вызове) они заменяются на фактические (см. разд. 7)
7. Обращение к функциям (их вызов)
voidmain()
{
……………………………………………………………….
int_toch = perv_obr(v_pred)-perv_obr(n_pred;// Точное значение интеграла
…………………………………………………………………..
prib_gauss = gauss_4(n_pred, v_pred, fun, prec);
………………………………………………………
prib_nyut = nyut_k_4(n_pred, v_pred, fun, prec );
//Здесь n_pred, v_pred, fun, prec –соответствующие фактические параметры (нижний и верхний пределы, подынтегральная функция и точность)
// Точность prec вводится с клавиатуры
……………………………………………………………
}
8. Распечатка файла, содержащего результаты работы программы
Точное значение интеграла = 1.370119928
Требуемая точность вычисления интеграла = 0.10000000
Гаусс для n = 4 Интеграл = 1.370020242 К-во обращений 24
Ньютон-К для n = 4 Интеграл = 1.371414377 К-во обращений 26
Выйгрыш Гаусс4 к Ньютон4 = 1.08333
______________________________________________________
Точное значение интеграла = 1.370119928
Требуемая точность вычисления интеграла = 0.01000000
Гаусс для n = 4 Интеграл = 1.370020242 К-во обращений 24
Ньютон-К для n = 4 Интеграл = 1.370184616 К-во обращений 59
Выигрыш Гаусс4 к Ньютон4 = 2.45833
______________________________________________________
Точное значение интеграла = 1.370119928
Требуемая точность вычисления интеграла = 0.00100000
Гаусс для n = 4 Интеграл = 1.370117696 К-во обращений 56
Ньютон-К для n = 4 Интеграл = 1.370121830 К-во обращений 124
Выигрыш Гаусс4 к Ньютон4 = 2.21429
9. Схема алгоритма метода Ньютона – Котеса
 |
10. Схема алгоритма метода Гаусса
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.