Построение графа, состоящего из 5 изолированных компонентов. Построение связанного графа из 13 вершин, содержащего 3 точки сочленения так, чтобы они не были смежными

Контрольная работа №1

Задание 1

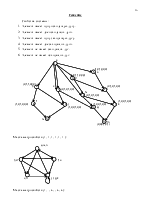
Построить граф, состоящий из 5 изолированных компонент мощностью 3, 5, 5, 6, 6 и 3 изолированных вершин. Во всем графе должно быть 3 истока, 3 стока, 2 висячие вершины, 4 регулярные вершины, три из которых имеют степени 3, 4, 5. Максимальная степень кратности графа должна быть 5. В графе должно быть > 5 пар противоположных дуг.

В отчете представить построенный граф с выделением всех построенных элементов. Написать полустепени исхода и захода для каждой вершины.

Решение

Изолированные вершины: 1, 2, 3

Вершины изолированных компонент:

4, 5, 6 (мощность 3);

7, 8, 9, 10, 11 (мощность 5);

11, 12, 13, 14, 15, 16 (мощность 5);

17, 18, 19, 20, 21, 22 (мощность 6);

23, 24, 25, 26, 27, 28 (мощность 6).

Вершины истоки: 4, 9, 14.

Вершины - стоки: 7, 10, 13.

Висячие вершины: 5, 6, 22.

Регулярные вершины: 8(степень 2), 12(степень 3), 18(степень 4),

23(степень 5).

Пары противоположно направленных дуг:

12-15, 15-12;

15-16, 16-15;

17-18, 18-17;

18-19, 19-18;

18-21, 21-18;

23-24, 24-23;

23-26, 26-23;

23-27, 27-23;

23-28, 28-23.

Полустепени исхода и захода вершин:

Задание 2

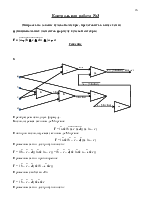
Построить ориентированный граф из 7 вершин и 14 дуг, содержащих один исток, один сток, одну изолированную вершину, одну регулярную вершину, одну петлю, пару одинаково направленных дуг, пару противоположно направленных дуг. С истоком и со стоком должно быть связано более двух дуг.

          Построить и проанализировать следующие способы представления графов: матрица смежности, матрица инцидентности, матрица окрестностей вершин по входам и выходам, список дуг. В отчете представить построенный граф и матричные представления графа с описанием (1 граф и 5 матриц: VV, VU, FО, FI, IО).

Решение

Изолированные вершины: 3.

Вершины истоки: 5.

Вершины - стоки: 2.

Регулярные вершины: 4.

Пары противоположно направленных дуг: 2-13.

Пары одинаково направленных дуг: 9-10.

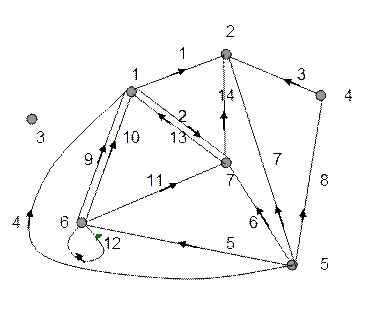
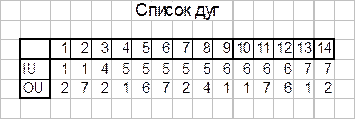
Проанализируем полученные данные.

Матрица смежности:

Единица в 6-ой строке на диагонали говорит о том, что вершина 6 имеет дугу-петлю. Вершины 1 и 7 имеют противоположно направленные дуги, т.к. соответствующие элементы матрицы, симметричные главной диагонали, заполнены. В графе имеются две кратные (одинаково направленные) дуги, от  6-ой к 1-ой вершине, соответственно в 6-ой строке 1-го столбца стоит 2. Строки матрицы соответствуют выходным окрестностям вершин, а столбцы– входным. Сумма элементов по строке равна полустепени исхода соответствующей вершины, а сумма элементов по столбцу – полустепени захода. Вершине–истоку 5 соответствует нулевой столбец 5 и ненулевая строка 5, а  вершине–стоку 2 соответствует ненулевой столбец 2 и нулевая строка 2. Изолированной вершине 3 соответствуют нулевой столбец 3 и нулевая строка 3.

Матрица инцидентности:

Дуге-петле 12 в матрице соответствует единственная 1 в 12-ом столбце, расположенная в 6-ой строке (с номером вершины 6, которой она принадлежит). Столбцы 9 и 10 одинаковы, следовательно, соответствующие дуги кратные. Столбцы 2 и 13 станут одинаковыми, если в них поменять местами 1 и -1, следовательно, соответствующие им дуги противоположно направленные. Количество -1 в любой строке равно полустепени исхода, а количество 1 - полустепени захода соответствующих вершин. Изолированной вершине 3 соответствует 3-я нулевая строка. Вершине-истоку 5 соответствует 5-ая строку, содержащая только -1 и 0, а вершине-стоку 2 – 2-ая строка, содержащая только 1 и 0. Регулярной вершине 4 соответствует 4-ая строка, содержащая равное количество (по одной) 1 и -1.

Матрицы окрестностей

Массив FI матрицы окрестности соответствует массиву  IU матрицы дуг, а массив KAO – массиву OU соответственно.

Задание 3

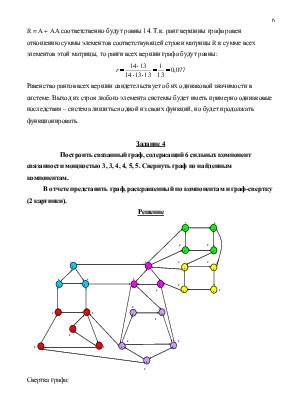
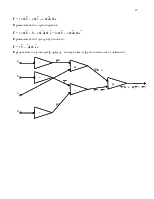
Построить связанный граф из 13 вершин, но содержащий 3 точки сочленения так, чтобы они не были смежными. Рассчитать ранги вершин этого графа.

В отчете представить построенный граф с выделенными точками сочленения и подписанными рангами каждой вершины (1 картинка).

Решение

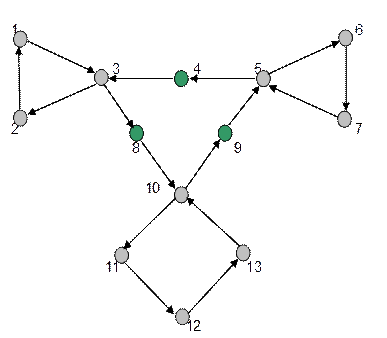
Очевидно, что от каждой вершины построенного связанного графа имеется путь к любой другой его вершине. Значит, все элементы матрицы достижимости А – единицы:

Тогда все элементы матрицы АА будут равны 13, а элементы матрицы

R = A + AA соответственно будут равны 14. Т.к. ранг вершины графа равен отношению суммы элементов соответствующей строки матрицы R к сумме