Применение метода динамического программирования для решения задачи оптимального распределения средств, направляемых на расширение производства

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА

Кафедра «Информационная безопасность»

Лабораторная работа №3

Решение задачи оптимизации производства методом динамического программирования

Выполнил студент

группы ЭиП-420

Лазарев А.А.

Проверил:

Баландин А.В.

Челябинск, 2008 г.

Цель работы:

Получение навыков применения метода динамического программирования для решения задачи оптимального распределения средств, направляемых на расширение производства.

Задание:

Исходный запас средств K=10. Требуется распределить его оптимальным образом между пятью предприятиями (m=5). Функции дохода φ_i(x) определяются при помощи таблицы 1 и поправочных коэффициентов α_i следующим образом:

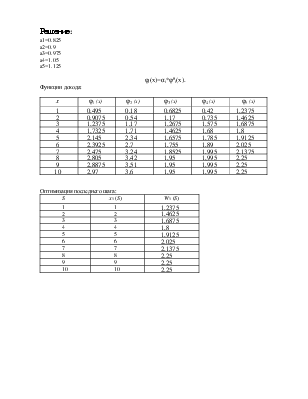
φ_i(x)=α_i*φ⁰­­_i(x).

Коэффициенты α_i определяются для каждого студента согласно его номеру (k) в списке группы:

α=(1+i/10)*(40-k)/40, i=1,…,5.

Таблица 1

x	φ0­­1 (x)	φ0­­2 (x)	φ0­­3 (x)	φ0­­4 (x)	φ0­­5 (x)
1	0,6	0,2	0,7	0,4	1,1
2	1,1	0,6	1,2	0,7	1,3
3	1,5	1,3	1,3	1,5	1,5
4	2,1	1,9	1,5	1,6	1,6
5	2,6	2,6	1,7	1,7	1,7
6	2,9	3,0	1,8	1,8	1,8
7	3,0	3,6	1,9	1,9	1,9
8	3,4	3,8	2,0	1,9	2,0
9	3,5	3,9	2,0	1,9	2,0
10	3,6	4,0	2,0	1,9	2,0

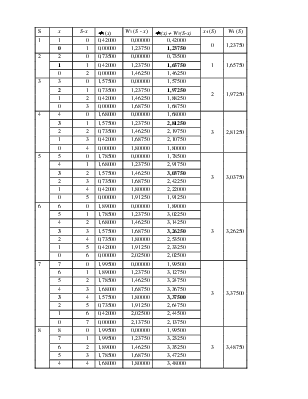
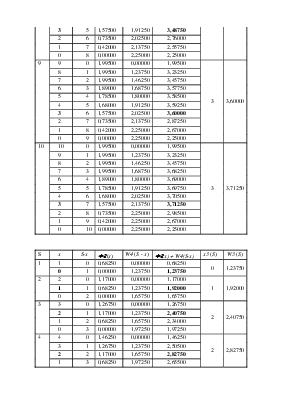
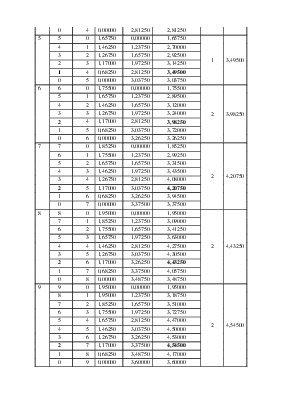
Условные обозначения:

K - запас средств\ресурсов

P - предприятия, между которыми требуется разделить средства

x - средства, вложенный в предприятие - шаговые управления (оптимальное управление, когда доход максимальный)

φ(х) - доход от предприятия в зависимости от вложенных в него средств

m - шаги решения задачи

S - наличный запас еще не вложенных средств

W(S) - условный оптимальный выигрыш

x(S) - соответствующее W(S) условное оптимальное управление

Решение:

a1=0.825

a2=0.9

a3=0.975

a4=1.05

a5=1.125

φ_i(x)=α_i*φ⁰­­_i(x).

Функции дохода:

x	φ­­1 (x)	φ­­2 (x)	φ­3 (x)	φ4 (x)	φ­­5 (x)
1	0,495	0,18	0,6825	0,42	1,2375
2	0,9075	0,54	1,17	0,735	1,4625
3	1,2375	1,17	1,2675	1,575	1,6875
4	1,7325	1,71	1,4625	1,68	1,8
5	2,145	2,34	1,6575	1,785	1,9125
6	2,3925	2,7	1,755	1,89	2,025
7	2,475	3,24	1,8525	1,995	2,1375
8	2,805	3,42	1,95	1,995	2,25
9	2,8875	3,51	1,95	1,995	2,25
10	2,97	3,6	1,95	1,995	2,25

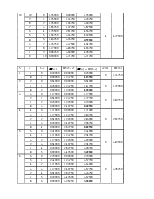
Оптимизация последнего шага:

S	x5 (S)	W5 (S)
1	1	1,2375
2	2	1,4625
3	3	1,6875
4	4	1,8
5	5	1,9125
6	6	2,025
7	7	2,1375
8	8	2,25
9	9	2,25
10	10	2,25