МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ ЭКОНОМИКИ И ПРЕДПРИНИМАТЕЛЬСТВА
Кафедра «Информационной безопасности»
ОТЧЕТ
по лабораторной работе:
«Решение линейной задачи оптимизации производства симплексным методом»
Выполнил: Лазарев А.А.
группа ЭиП-520
Проверил: Баландин А.В.
Челябинск 2008
Задание:
Задана линейная модель задачи оптимизации проектного решения в виде:
,![]()
при условиях
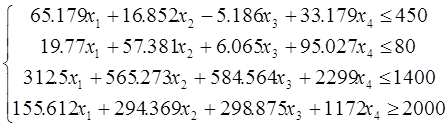 ;
;
![]()
![]()
![]()
![]()
Необходимо найти оптимальное решение данной задачи линейного программирования.
Прежде всего, перейдём от системы неравенств к системе
уравнений. Для этого введём добавочные переменные x5, x6,
x7, x8 (![]()
![]()
![]()
![]() ):
):
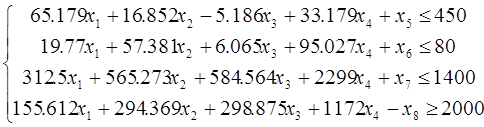
Далее находим первоначальный опорный план (допустимое базисное решение) методом искусственного базиса.
Если в качестве базиса взять x5, x6, x7, x8, то x1, x2, x3, x4 будут свободными. Положим свободные переменные равными нулю, тогда будет получено следующее базисное решение {450, 80, 1400, -2000}. Это решение не является допустимым, так как x8<0.
Применяем метод искусственного базиса.
Введём в четвертое уравнение искусственную переменную x9 и решим вспомогательную задачу линейного программирования, заключающуюся в минимизации целевой функции f(x)=x9 (что эквивалентно максимизации целевой функции f*(x)=-f(x)=-x9).
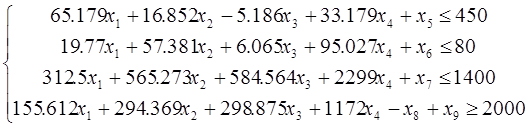
Первоначальное допустимое базисное решение для вспомогательной задачи будет
{x5, x6, x7, x9} = {450, 80, 1400, 2000}.
Составим и заполним первую симплекс-таблицу для вспомогательной задачи.
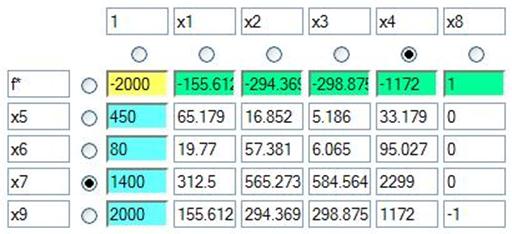
Проведем преобразования:
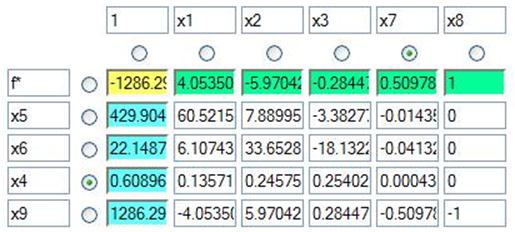
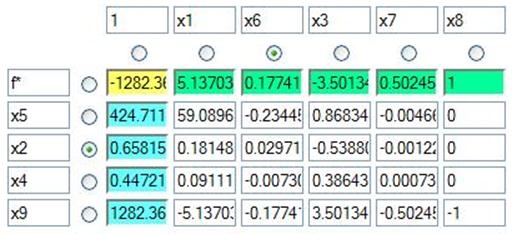
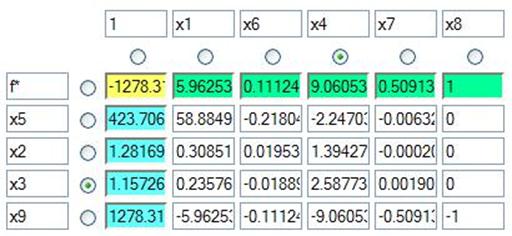
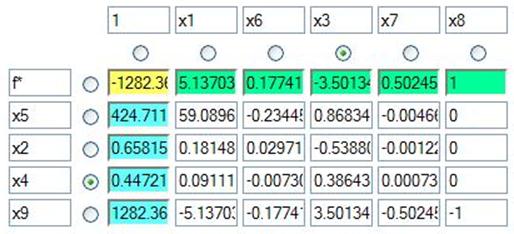
Так как f≠0 задача не имеет решений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.