Непараметричні тести. Дисперсійний аналіз. Факторний аналіз

Лекція 9.  Теми: «Непараметричні тести. Дисперсійний аналіз»

Непараметричні тести

План лекції

1.  Порівняння параметричних та непараметричних критеріїв

2.  Розрахунок U-критерію Манна-Уітні

3.  Непараметричні тести в пакеті SPSS

1. Параметричні та непараметричні критерії розбіжностей

n Критерій розбіжності називають параметричним, якщо він ґрунтується на наявному вигляді розподілу генеральної сукупності (як правило, нормальному) або використовує параметри цієї сукупності (середні, дисперсії тощо).

n Критерій розбіжності називають непараметричним, якщо він не базується на припущенні щодо виду розподілу генеральної сукупності та не використовує параметри цієї сукупності.

n За умови нормального розподілу генеральної сукупності параметричні критерії мають більшу потужність у порівнянні з непараметричними, вони здатні з більшою вірогідністю відкидати нульову гіпотезу, якщо вона невірна. Тому у випадках, коли вибірки взято з нормально розподілених генеральних сукупностей, варто віддавати перевагу параметричним критеріям.

n Проте практика показує, що розподіл переважної більшості даних, одержуваних у соціологічних опитуваннях, не відповідає нормальному розподілу, тому застосування параметричних критеріїв для аналізу результатів соціологічних досліджень може призвести до помилок у статистичних висновках. У таких випадках зазвичай застосовують непараметричні критерії.

У порівнянні з параметричними тестами непараметричне тестування має як певні переваги, так і недоліки.

Переваги

n Непараметричне тестування не потребує ніяких припущень щодо характеру розподілу генеральної сукупності, з якої взято досліджувану вибірку.

n Методи непараметричного тестування можуть застосовуватися навіть тоді, коли вибірка дуже мала.

Недоліки

n У порівнянні з параметричними тестами отримані дані використовуються менш ефективно. Потужність (тобто ймовірність відхилення нульової гіпотези, коли вірна альтернативна) непараметричних тестів нижча, ніж параметричних. Із цієї причини аналітики вважають, що застосування параметричних тестів є бажанішим у тих випадках, коли може бути зроблено необхідні припущення щодо генеральної сукупності.

Треба пам’ятати, що непараметричні методи найбільш прийнятні, коли обсяг вибірок малий. Якщо даних багато (наприклад, n >100), то можна застосовувати параметричні статистики, оскільки для великих вибірок вибіркові середні підкоряються нормальному закону, навіть якщо досліджувана змінна не є нормальною. Таким чином, параметричні методи, які мають вищу статистичну потужність, завжди підходять для великих вибірок. Проте в роботі соціолога інколи виникають ситуації, коли треба дослідити певні малочисленні групи та виділити характерні риси, які відрізняють їх від інших (наприклад, дослідження інтелектуальної еліти). У таких випадках застосування непараметричних тестів може бути дуже корисним для виявлення статистичної значущості розбіжностей.

2. U-тест Манна-Уітні

n U-тест Манна - Уітні (англ. Mann – Whitney U-test)  – статистичний критерій, що застосовується для оцінки розбіжностей між двома вибірками за рівнем деякої ознаки, що виміряна інтервальною або порядковою шкалою. Інші назви: критерій Манна – Уітні – Уілкоксона (англ. Mann –Whitney – Wilcoxon, MWW), критерій суми рангів Уілкоксона (англ. Wilcoxon rank-sum test), критерій Уілкоксона – Манна – Уітні (англ. Wilcoxon – Mann – Whitney test). Це найвідоміший і найпоширеніший тест непараметричного порівняння двох незалежних вибірок.

Розглянемо принцип, який є основою U-тесту. Для цього методом випадкового відбору виберемо 15 анкет з масиву st09.sav (див. рис.), та перевіримо гіпотезу про більш негативне ставлення жінок до абортів у порівнянні з чоловіками.

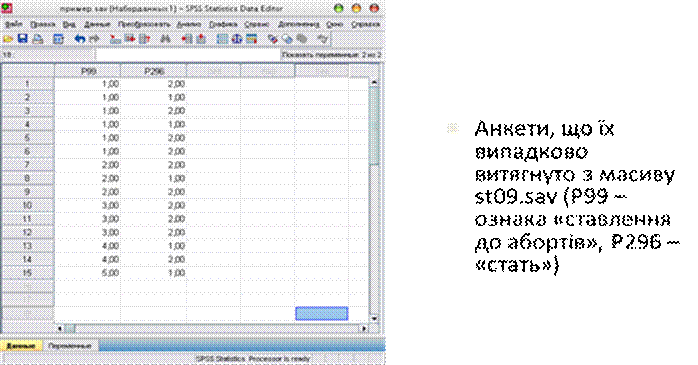
n Позначимо кожний елемент першої групи символом x, а другий - символом y. Тоді загальний упорядкований за зростанням чисельних величин ряд можна представити так:

y  x  y x y y y  x y y y y  x y x  - елементи першої (x) та другої (y) вибірки.

1  1 1 1 1 1 2 2 2 3 3 3 4 4 5   - значення досліджуваної ознаки.

n Якби  впорядкований ряд, складений за даними двох вибірок, прийняв би вигляд

x x x x x x x x x y y y y y y,

   то дві вибірки значуще розрізнялися б між собою. Таке розташування називається ідеальним. Критерій U базується на підрахунку порушень у розташуванні чисел в упорядкованому емпіричному ряді в порівнянні з ідеальним рядом.

Для застосування U-критерію Манна - Уітні потрібно виконати наступні операції.

1. Скласти з обох вибірок єдиний ранжований ряд (порівняти вибірки між собою, розставивши їх елементи за ступенем наростанням ознаки й приписавши меншому значенню менший ранг). Потім треба розділити єдиний ранжований ряд на два, що містять відповідно одиниці з першої та другої вибірок (див.табл.1). При цьому треба мати на увазі, що загальна кількість рангів дорівнює N  = n1 + n2, де n1 – кількість одиниць у першій вибірці, а n2  – кількість одиниць у другій вибірці.

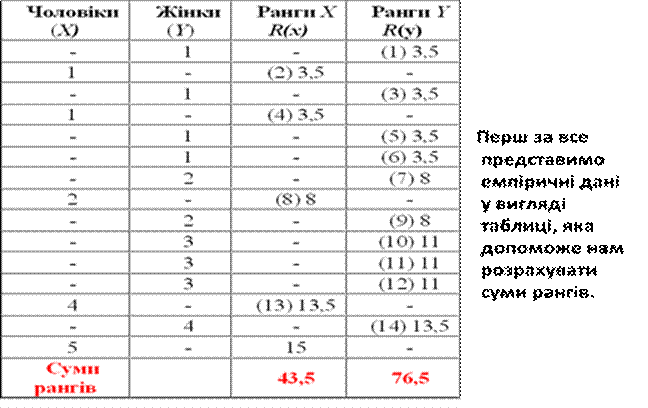
2. Підрахувати окремо суму рангів, що відповідають елементам першої вибірки, і окремо – елементам другої вибірки. Визначити більшу із двох рангових сум (R_max).

Сума рангів:

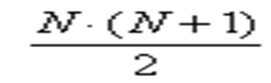
Перевіримо правильність нашого ранжування. Ми отримали суму рангів:

43,5 + 76,5 = 120.

Сума рангів розраховується за формулою:

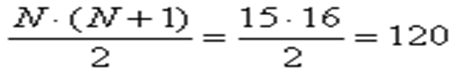
Розрахункові суми випадків збігаються, значить, ранжування було проведено правильно.

У таблиці можна побачити, що рангова сума в першій групі R1 = 43,4, а в другій R2 = 76,5.

3. Визначити емпіричне значення U-критерію Манна-Уітні. Для цього обчислюємо два значення:

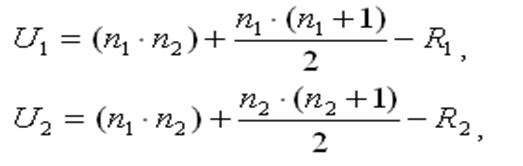
   де n1 – кількість респондентів у першій вибірці,

n2 – кількість респондентів у другій вибірці,

R1 – сума рангів у першій вибірці,

R2 – сума рангів у другій вибірці.

    Емпіричним значенням U-критерію Манна-Уітні вважається найменше з U1 і U2.

Обчислюємо емпіричне значення
U-критерію. U_емп = min {U₁; U₂}

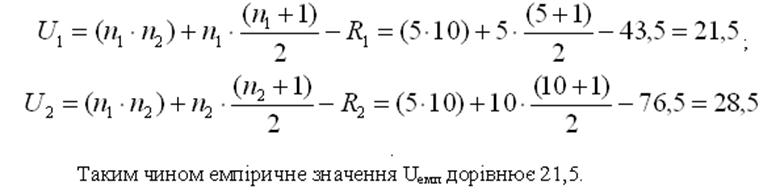
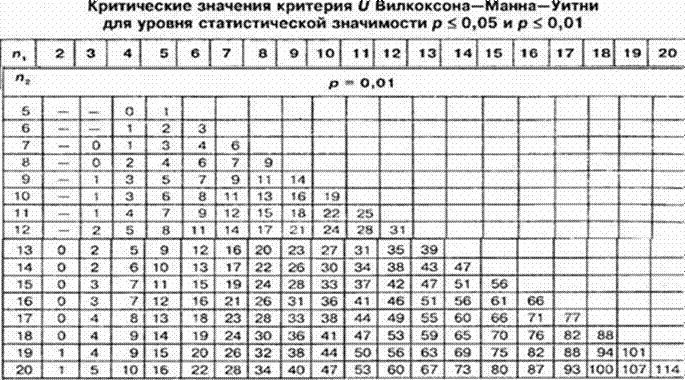
4. За таблицею визначити критичне значення критерію для n₁ та n₂ для обраного рівня статистичної значущості.

    Якщо отримане значення U_емп менше табличного або дорівнює йому, це означає наявність істотної розбіжності між рівнем ознаки у розглянутих вибірках.

    Якщо ж отримане значення U_емп більше табличного, приймається нульова гіпотеза - робиться висновок, що розбіжностей не виявлено. При цьому вірогідність розходжень тим вища, чим менше значення U_емп.

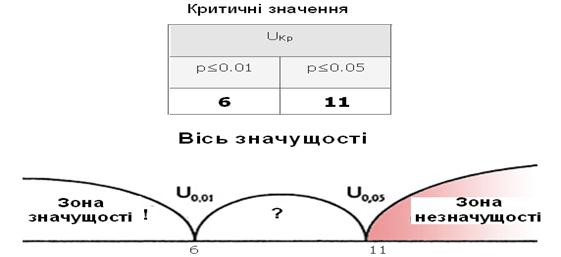
Шукаємо критичне значення у таблиці (див. далі). Число на перетині розміру найбільшої (sіze of the largest sample) і найменшої (sіze of the smallest sample) з наших вибірок є критичним значенням коефіцієнта Манна-Уитни. У нашому випадку розмір найбільшої вибірки 10, найменшої – 5. Критичне значення Uкрит = 11 за p≤ 0,05,  Uкрит = 6 за p≤ 0,01.

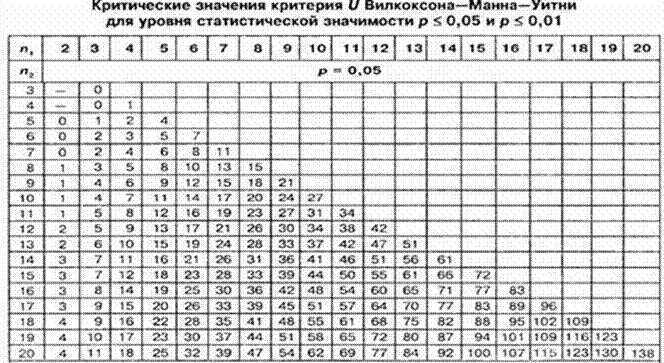
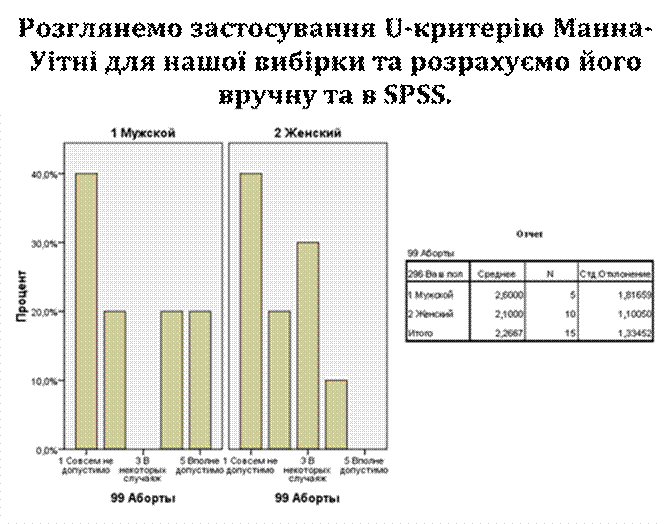
Висновок. Отримане емпіричне значення Uемп = 21,5 є більшим за критичне, тобто статистично значущих розбіжностей не виявлено (див. рис.).

Дисперсійний    аналіз

План лекції

1. Однофакторний дисперсійний аналіз

Дисперсійний аналіз

дозволяє визначити статистичну достовірність розбіжностей між кількома вибірками шляхом порівняння середніх значень.

Іншими словами, дисперсійний аналіз може слугувати перевіркою гіпотези про розбіжність середніх значень у декількох групах та дозволяє розподілити всю сукупність груп на певну кількість кластерів, які значуще відрізняються за значенням середніх (тест Дункана, докладніше див.: Бююль А., Цёфель П. SPSS: Искусство обработки информации, анализ статистических данных и восстановление скрытых закономерностей, гл.13,п.3).

Розглянемо застосування дисперсійного аналізу для дослідження статусних домагань українських студентів (масив st06.sav).