Кореляційний аналіз у соціології. Двовимірний розподіл двох ознак: наочне зображення, коефіцієнти кореляції. Способи візуалізації дво/тривимірних розподілів

Кислова О. М.Курс «Методи аналізу соціологічної інформації»

Лекція 3. Кореляційний аналіз

План лекції

1.  Кореляційний аналіз у соціології: сутність кореляційної залежності, вигляд кореляційної таблиці.

2. Двовимірний розподіл двох ознак: наочне зображення, коефіцієнти кореляції.

3.  Способи візуалізації дво/тривимірних розподілів.

Кореляційний аналіз − сукупність методів виявлення кореляційної залежності між двома ознаками.

Мета кореляційного аналізу – забезпечити отримання інформації про одну змінну за допомогою іншої змінної.

Особливості кореляційної залежності

Функціональна залежність: одному значенню “Х” відповідає одне значення “У”;

Кореляційна залежність: одному значенню “Х” відповідають декілька значень “У”.

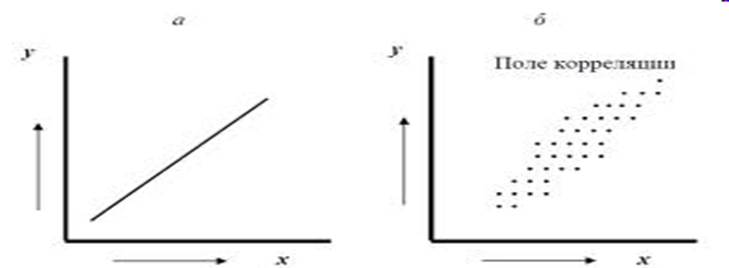
Кореляційна залежність - це залежність, де вплив окремих факторів проявляється тільки як тенденція (у середньому) при масовому спостереженні фактичних даних.

Різновиди кореляційної залежності:

•  Пряма:

Зі збільшенням/зменшенням значення “Х”, збільшуються/зменшуються значення “У”;

•  Зворотна:

Зі збільшенням/зменшенням значення “Х”, зменшуються/зменшуються значення “У”

Різновиди кореляційної залежності:

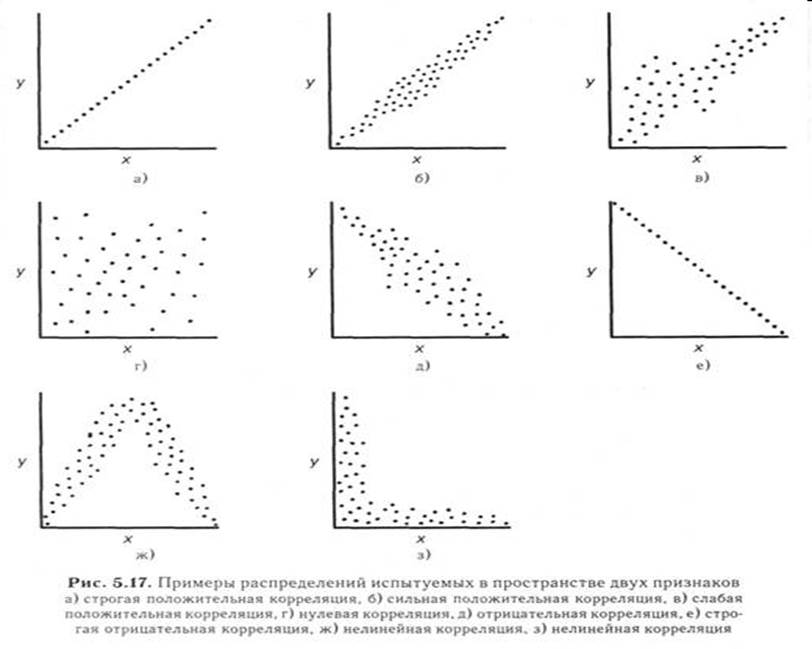
•  Пряма:

Зі збільшенням значення “Х”, збільшуються значення “У”;

•  Зворотна:

Зі збільшенням значення “Х”, зменшуються значення “У”

В залежності від кількості досліджуваних ознак кореляційний аналіз поділяють на:

•  кореляційний аналіз двох ознак;

•  кореляційний аналіз трьох ознак;

•  кореляційний аналіз  чотирьох або більше ознак (багатовимірний кореляційний аналіз).

•   

Кореляційний аналіз двох ознак

( = аналіз взаємозв'язку двох ознак

= аналіз двовимірних розподілів).

Основні практичні прийоми кореляційного аналізу:

1) побудова кореляційної таблиці та/або побудова кореляційного поля;

    2) обчислення та інтерпретація коефіцієнтів кореляції.

Найпростішим прийомом виявлення зв'язку між двома ознаками є побудова кореляційної таблиці (тобто двовимірного розподілу)

 Синонимічні назви

Кореляційна таблиця =

 двовимірний розподіл =

 крос-табуляція

Двовимірна частотна таблиця (чи кореляційна таблиця, таблиця зв'язаності) – це матриця, у якій на перетині i-го рядка й j-го стовпця знаходиться nij – частота сумісної появи відповідних значень двох ознак xi та yj.

Загальний вигляд кореляційної таблиці

	Y				Результат за рядками N (x)
X	y1	y2	…	yj
x1	n11	n12	…	n1j	N(x1)
x2	n21	n22	…	n2j	N(x2)
xi	ni1	ni2	…	nij	N(xi)
Результат за стовпцями N(y)	N (y1)	N(y2)	…	N(yi)	N

Таблиця зв'язаності

СУМІСНИЙ РОЗПОДІЛ ЗМІННИХ «СТАТЬ РЕСПОНДЕНТА" Й «ЗАДОВОЛЕНІСТЬ ШЛЮБОМ" (АБСОЛЮТНІ ЧАСТОТИ)
Стать респондента	Задоволеність шлюбом
	Висока	Середня	Низька	Всього
Чоловіча	40	30	10	80
Жіноча	20	40	20	80
Всього	60	70	30	160

Наочним зображенням кореляційної таблиці виступає кореляційне поле (діаграма розсіювання). Діаграма розсіювання представляє графік, де на осі абсцис відкладають значення Х, на осі ордінат − У, а точками вказується поєднання Х та У. За розташуванням точок, їх концентрацією в певному напрямку можна судити про наявність зв'язку. Таким чином, кореляційне поле (діаграма розсіювання) дозволяє здійснити графічну інтерпретацію взаємозв'язку ознак.
.

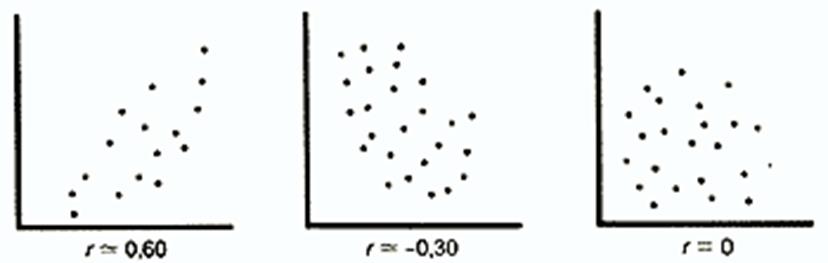
ПРИКЛАД.
Діаграма розсіювання, що демонструє кореляційну залежність ознак «соціальний щабель батьків» і «соціальна сходинка, на яку хотіли б потрапити» (Kendall's tau-b = 0,355).

Кореляційне поле отримують в результаті побудови діаграми розсіювання

   (в SPSS для побудови такої діаграми існує команда Graphs → Scatterplot → Simple.

Коефіцієнти кореляції

 #10. ПОЧУТТЯ ВЛАСНОЇ ГІДНОСТІ
 #9. УРАХУВАННЯ УСПІШНОСТІ ПРИ МАЙБУТНЬОМУ ПРАЦЕВЛАШТУВАННІ


Коефіцієнт Хі-квадрат                  196.386 (значущий на рівні 1%)
  Кількість ступенів свободи                    9
  Коефіцієнт Чупрова                       0.200
  Коефіцієнт Крамера                       0.200
 
 Коефіцієнт лямбда Гудмана
     вплив #10# на #9#             0.045
     вплив #9# на #10#             0.091
 Коефіцієнт кореляції Пірсона                 0.314 (значущий 1%)
  Коеф. рангової кореляції Спірмена        0.313 (значущий 1%)

Рівень значущості та показники коефіцієнтів

Коефіцієнт Хі-квадрат  196.386 (значущий на рівні 1%)

Слід зазначити, що для коефіцієнтів кореляції окрім власне свого значення (Хі-квадрат=196,386) розраховують рівень значущості  коефіцієнта (0,05; 0,01; 0,005; 0,001).

•  Базуючись на ймовірнісному принципі, рівень значущості дозволяє зазначити ймовірність помилки про наявність зв′язку між ознаками і т.д. 

•  Чим ближче рівень значущості до нуля, тим менше ймовірність помилки.

Зверніть увагу!

•  Для різних типів шкал використовують розрахунок різних коефіцієнтів кореляції;

•  Якщо у двовимірному розподілі присутні ознаки, вимірювані різними типами шкал (номінальна і порядкова, порядкова і метрична, номінальна і метрична), слід аналізувати коефіцієнти кореляції, які розраховуються для найнижчого рівня шкалювання.

Критерій Хі-квадрат

•  Особливості показника:

Зазначає наявність/відсутність зв′язку між двома ознаками;

Розраховується на основі співставлення теоретичної моделі таблиці (коли зв′язок відсутній) з емпіричною моделлю (емпірична таблиця);

Якщо зазначається, що Хі-квадрат не є значущим на рівні 1% чи 5% - це свідоцтво відсутності звя′зку між ознаками;

Приймає значення від 0 до + ∞;

Коефіцієнт кореляції Пірсона

Для кількісної оцінки щільності зв'язку використовують лінійний коефіцієнт кореляції Пірсона.
     Коефіцієнт кореляції Пірсона може приймати значення в інтервалі від -1 до + 1.

    Якщо ж «r» набув значення, що близьке до «0», це - підстава стверджувати про відсутність лінійного зв'язку між досліджуваними змінними.

    Однак у цьому випадку можлива нелінійна взаєзалежність, що потребує додаткової перевірки та застосування інших коефіцієнтів.

Для словесного опису значень коефіцієнта кореляції можна застосовувати наступну таблицю:

Значення коефіцієнта кореляції r	Інтерпретація (характеристика сили зв'язку)
0 < г <= 0,2	Дуже слабка кореляція (відсутність зв’язку між перемінними)
0,2 < г <= 0,5	Слабка кореляція
0,5 < г <= 0,7	Середня (помірна) кореляція
0,7 < г <= 0,9	Сильна кореляція
0,9 < г <= 1	Дуже сильна кореляція

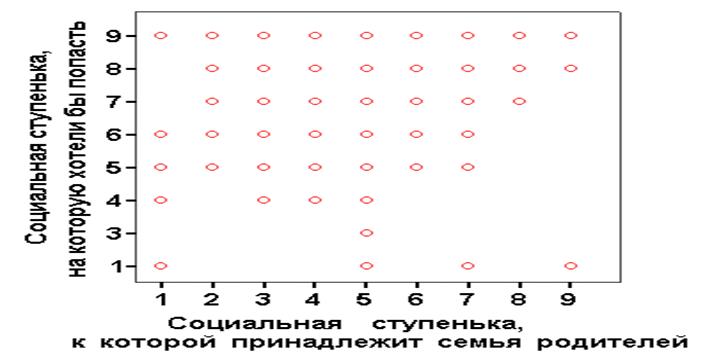
Коефіцієнт кореляції Пірсона та візуалізація кореляційної залежності ознак.
Зверніть увагу, що коефіцієнт кореляції Пірсона відображає лінійну залежність (верхній рядок), але не описує криву залежності (середній рядок), і не підходить для опису складних, нелінійних залежностей (нижній рядок).