Управление кратной синхронизацией роторов плоского движения платформы виброустановки

были введены датчики положения роторов, информация от которых передавалась в компьютер, где в реальном масштабе времени рассчитывались текущие значения управляющих сигналов.

Динамика одномерного движения указанного вибрационного стенда моделировалась на компьютере в программной среде MATLAB, причем исследовался режим кратной синхронизации при традиционном управлении с помощью постоянных по величине управляющих моментах М₁=2Н·м, М₂=1Н·м. Модель динамики движения стенда вдоль вертикальной оси имеет вид:

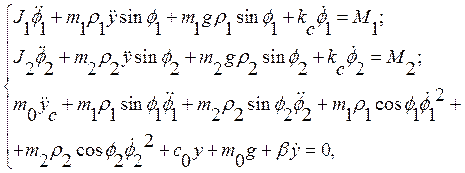             (1.1)

где: φ₁,φ₂ - углы вращения роторов, измеряемые от нижнего вертикального положения;  y - вертикальная координата центра платформы; m_пл,m₁,m₂ - массы платформы и роторов соответственно; J₁ ,J₂ - моменты инерции роторов; ρ₁, ρ₂ - эксцентриситеты  роторов; с₀ -жесткость пружин, g – ускорение свободного падения; k_c-коэффициент трения в подшипниках; β-коэффициент сопротивления линейного демпфирующего элемента; M₁, М₂ –управляющие моменты электрических двигателей; m₀=m_пл+ 2m.

Как видно из уравнения (1.1) модель динамики вибрационной системы является существенно нелинейной и взаимосвязанной, что затрудняет управление такой системой.

Графики изменения вертикальной координаты платформы y, м (а); скоростей роторов (в) и приведенного сдвига фаз (б) представлены на рис. 1.1.

Из рисунка видно, что для скоростей имеет место приближенное равенство  и приведенный сдвиг фаз  приблизительно равен  -3π.

Условия на массоинерционные параметры двухроторной системы совершающей колебания вдоль оси, при котором возможен эффект двукратной самосинхронизации, были получены в работе Н.П. Ярошевича [19] и имеют следующий вид:

 ,                           (1.2)

где , где m₁, m₂ – массы роторов; m_пл – масса платформы; ρ₁, ρ₂ – эксцентриситеты роторов; J₁ – момент инерции первого ротора; g – ускорение свободного падения; М_Д1, М _Д2 – вращающие моменты электродвигателей;  М_С1,    М _С2 – моменты сил сопротивления вращению.

Рис. 1.1.

Предположим, что М_Сi  пропорциональны скоростям вращения роторов:

 ,

где к_с – коэффициент вязкого трения в подшипнике.

Для стенда СВ-1 значения параметров следующие: m₁=m₂=1,5кг; m_пл =9кг;  ρ₁= ρ₂= 0,04м;  J₁=0,014кг·м²;  к_с=0,01; М_Д1=2Н·м;  М _Д2=1Н·м.

Очевидно, что условия (1.2) выполняются. При этом имеет место приближенная двукратная частотная и координатная синхронизация ()(рис.1.2 а)). В то же время, при присоединении к несущей платформе дополнительного груза (m_г=1кг) кратная самосинхронизация нарушается: приведенный сдвиг фаз  (рис.1.2 б)). Как показано ниже отсутствие кратной самосинхронизации так же имеет место при учете упругости карданных валов, соединяющих двигатель с неуравновешенным ротором (рис.1.2. в)). На рис. 1.2 показаны результаты моделирования при рассмотрении возможности