Пленочные элементы интегральных микросхем и микросборок
К пленочным элементам относят: резисторы, конденсаторы, проводники, линии с распределенными параметрами и пленки из диэлектрических материалов.
В зависимости от толщины пленки бывают:
Токая пленка – до 10 микрон;
Толстая пленка – от 10 микрон и более.
Толстые пленки изготавливают с помощью паст. Тонкие пленки – все виды получения пленок.
Кроме толщины все пленки различаются материалом, технологией изготовления и электрофизическими параметрами (у тонких пленок имеют нелинейную зависимость) и общими требованиями конструкции пленочных элементов (минимальные габаритные размеры, стабильность, воспроизводимость характеристик в процессе производства, совместимость технологических процессов с технологическими процессами изделий в состав которых они будут входить.
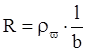 ,
,
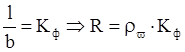
Если у нас квадратная форма, то: ![]() .
.
Основными электрическими параметрами пленочного
резистора являются: R, ![]() ,Кф,
,Кф,
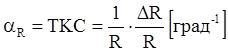 , удельная мощность
, удельная мощность 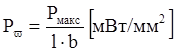 .
.
Расчет тонкопленочных резисторов
Исходные данные:
Номинальная величина сопротивления – R;
Допуск на номинал – gR;
Диапазон рабочих
температур – ![]() ;
;
Точность выполнения линейных размеров –Db, Dl;
Технологические ограничения:
Мощность, рассеиваемая на каждом резисторе – P.
В зависимости от точности изготовления резистора выбирается тот или иной способ формирования конфигурации:
При gR³10 % можно воспользоваться масочным способом;
При gR£5 % фотолитографическим методом.
Выбрав метод формирования конфигурации определяют Db и Dl, а соответственно и технологические ограничения.
Рекомендуется следующая последовательность проведения расчета:
1) Определяется соотношение: ![]() , если
получается больше 50 то рекомендуется изготавливать резисторы из двух различных
материалов. Для этого все резисторы разбивают на две группы:
, если
получается больше 50 то рекомендуется изготавливать резисторы из двух различных
материалов. Для этого все резисторы разбивают на две группы:
![]() первой группы меньше а,
первой группы меньше а,
![]() второй группы больше
значения сопротивления численно равного удельному электрическому сопротивлению:
второй группы больше
значения сопротивления численно равного удельному электрическому сопротивлению:
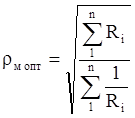 ,
,
![]() – номинал i-го
сопротивления,
– номинал i-го
сопротивления,
n – число резисторов в схеме.
После разбивки рассчитывают ![]() для каждой
группы в отдельности, потом делят и если а
меньше 50, то можно делать из одного материала.
для каждой
группы в отдельности, потом делят и если а
меньше 50, то можно делать из одного материала.
2) Выбираем материал резистивной пленки из таблицы с удельным сопротивлением близким к рассчитанному значению и соответственно с учетом рекомендуемого диапазона номинальных значений резисторов. При этом необходимо, чтобы температурная погрешность была мала, а удельная мощность Р0 велика.
3) Рассчитываем погрешности:
![]() ,
,
![]() – погрешность коэффициента формы,
– погрешность коэффициента формы,
![]() – погрешность воспроизведения
удельного сопротивления,
– погрешность воспроизведения
удельного сопротивления,
![]() – температурная погрешность,
– температурная погрешность,
![]() – погрешность, связанная со
старением пленки,
– погрешность, связанная со
старением пленки,
![]() – погрешность переходных
сопротивлений контактов.
– погрешность переходных
сопротивлений контактов.
В первом приближении ![]() .
.
Две последние составляющие важны для прецизионных резисторов и составляют (1–2)%.
![]() ,
,
![]() – температурный коэффициент
сокращения материала пленки,
– температурный коэффициент
сокращения материала пленки, ![]() задана.
задана.
![]() ;
;
4) Определяем коэффициент формы каждого резистора:![]() , если
, если ![]() , то резистор можно
выполнять прямоугольной формы, длина которого больше ширины, если
, то резистор можно
выполнять прямоугольной формы, длина которого больше ширины, если ![]() , то длина выполняется
меньше ширины, если
, то длина выполняется
меньше ширины, если ![]() , то резистор должен
иметь форму меандра.
, то резистор должен
иметь форму меандра.
Резисторы с коэффициентом формы меньше 0,1 занимают большие площади на подложке и выполнять их не рекомендуется.
5) Определяется ширина резистора, коэффициент формы которого больше 1:
![]()
![]() – технологическое минимальное
значение ширины, определяемое технологическими факторами,
– технологическое минимальное
значение ширины, определяемое технологическими факторами,
![]() – определяется заданной точностью
изготовления,
– определяется заданной точностью
изготовления,
![]() (по мощности) – обеспечение
необходимой мощности рассеяния.
(по мощности) – обеспечение
необходимой мощности рассеяния.
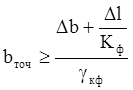 ,
,
Кф – берется в долях единицы.
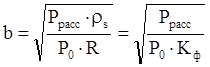 ,
,
Р0 – допустимая удельная мощность рассеяния резистора.
За ширину b принимают ближайшее
к ![]() большее значение, кратное шагу координатной
сетки h принятому для чертежа топологии (рекомендуется h=0,01 мм).
большее значение, кратное шагу координатной
сетки h принятому для чертежа топологии (рекомендуется h=0,01 мм).
6) Определяется длина резистора, имеющего коэффициент формы больше 1:
![]() ,
,
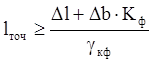 ,
, 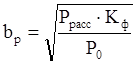 .
.
За длину lp берется большее значение кратное шагу координатной сетки.
7) Определяется ширина резистора с коэффициентом формы меньше 1:
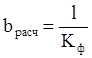 , полученное значение
, полученное значение ![]() округляется в большую сторону с точностью
до h. Таким образом получаем b
для каждого резистора.
округляется в большую сторону с точностью
до h. Таким образом получаем b
для каждого резистора.
Для прямоугольной формы резистора ![]() .
.
Если резистор состоит из резистивных полосок, то берется
сумма их, которая равняется ![]() .
.
Если Кф>10, значит резистор должен иметь форму меандр.
1) Определяется
длина средней линии ![]() .
.
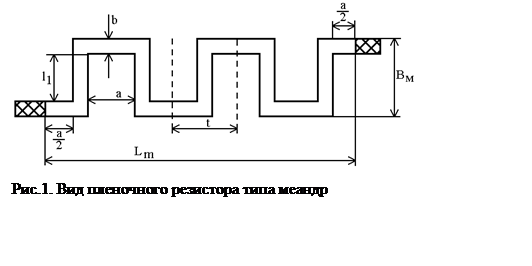
а – расстояние между резистивными полосками ,
t – шаг
одного звена (меандр) ![]() ,
,
Lm – длина контура меандр,
bm – ширина контура меандр.
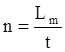 – число звеньев.
– число звеньев.
2) Определяется длина средней линии: ![]() .
.
3) Задается расстояние а с
учетом технологичных ограничений. Материал ![]() .
Оптимально а=b. Определяется оптимальное количество
звеньев:
.
Оптимально а=b. Определяется оптимальное количество
звеньев:
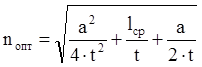 ,
,
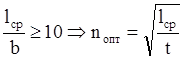 , вычислив величину nопт округляем до ближайшего целого числа.
, вычислив величину nопт округляем до ближайшего целого числа.
4) Определяется длина меандра:
![]() ,
, 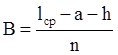 .
.
Расстояние а выбирается из конструктивных соображений. Оно должно удовлетворять условию:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.