Уравнение (13.13) является более компактным в части необходимых расчетов, однако несколько проигрывает по наглядности в сравнении с уравнением (13.12). Читатель может обосновать вывод уравнений (13.12) и (13.13) с помощью рис. 13.10. Можно использовать любое из двух уравнений, однако следует подчеркнуть следующее: ни уравнение (13.12), ни уравнение (13.13) не отвечают случаю, когда индикаторы верхнего и нижнего пределов включены в кодирование. Декодирование в подобном случае для различных значений п рассмотрено в учебном примере, приведенном ниже.
Важной областью применения принципа декодирования является преобразование выходного сигнала управляющей ЭВМ в аналоговый вид. Этот тип декодирования называется цифроаналоговым преобразованием выходного сигнала и представляет собой операцию, обратную аналого-цифровому преобразованию входного сигнала. Однако следует подчеркнуть, что цифроаналоговое преобразование выходных сигналов имеет не столь большое значение, как аналого-цифровое преобразование входных сигналов. Дело в том, что производственное оборудование в большинстве случаев включает преобразователь, который может воспринимать выходные сигналы от устройства управления, представленные в цифровом виде. В качестве примера здесь можно привести шаговый двигатель, которым оснащаются рабочие органы робота. ЭВМ устройства управления выдает дискретный ряд импульсов напряжения на шаговый двигатель, который обеспечивает перемещение рабочего органа на заданную величину. Следует также учесть, что измерение и контроль работы производственного оборудования занимают большую часть времени функционирования управляющей ЭВМ по сравнению со временем, затрачиваемым на формирование выходных сигналов. Это обусловливает большую важность аналого-цифрового преобразования по сравнению с цифроаналоговым.
Как аналого-цифровое, так и цифроаналоговое преобразование должны выполняться на периодической основе. Для выполнения преобразования требуется ограниченное количество времени. В промежутках между циклами преобразования управляющая ЭВМ выполняет другие функции." При этом следует определить значение переменной, которое должно быть выбрано между циклами преобразования. Очевидный алгоритм предполагает сохранять значение переменной на предварительно вычисленном уровне до завершения следующего цикла преобразования. Однако другим алгоритмом принимается во внимание скорость изменения переменного параметра, особенно в случае, когда скорость изменения велика. На рис. 13.11 приведено сравнение этих двух алгоритмов. Погрешность, возникающая между циклами преобразования, может превышать дискретность преобразования. Исследование этого вопроса входит в задачу теории дискретных систем, представляющую определенный интерес. Однако подробное изложение этой сложной проблемы выходит за рамки настоящей книги.
Рассматривая указанную проблему дальше, следует отметить, что аналоговые входные и выходные сигналы не имеют для роботов и автоматизированного производственного оборудования столь большого значения, как цифровые входные и выходные сигналы. Автоматическая коррекция технологических параметров формируется именно на основе анализа сочетания состояний цифровых логических сигналов, характеризующих технологический процесс, а не по уровню изменения аналоговых переменных. Управление промышленным оборудованием производится, как правило, с помощью дискретных логических функциональных выходных сигналов, а не ответных аналоговых сигналов. Действительно заводы с непрерывными технологическими процессами, как, например, химические, нефтеочистительные и цементные электростанции имеют множество критических аналоговых технологических параметров, которые подлежат тщательному контролю. Однако в робототехнике и автоматизированном производстве изделия, технологические процессы, а также параметры процесса управления в большинстве, случаев являются дискретными.
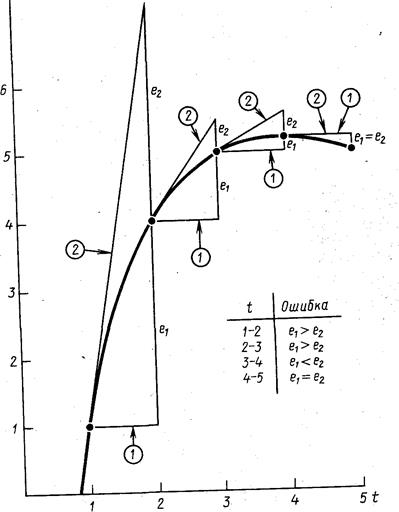
Рис. 13.11
Сравнение стратегий приближения аналоговой переменной при квантовании:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.