Диффузия в металлах. Феноменологическая теория диффузии. Атомная теория диффузии

ДИФФУЗИЯ В МЕТАЛЛАХ

Изучение диффузии в металлах и сплавах необходимо, во-первых, для понимания изменений, происходящих в твердых телах при высоких температурах, так как процессы диффузии во многом определяют кинетику процессов выделения фаз, окисления, ползучести и т. д., во-вторых, для получения сведений о поведении точечных дефектов в кристаллах.

Проблему изучения диффузии можно условно разделить на две части. В первой - феноменологической - металл рассматривают как континуум, т. е. пренебрегают его атомной структурой. При этом может быть рассмотрена большая часть структурных изменений, происходящих в результате диффузионных процессов. Кинетику изменений обычно описывают системой дифференциальных уравнений. При составлении уравнений используют предположения, впервые сделанные еще в 1855 г. Фиком. Во второй части – микроскопической – учитывают атомное строение и атомные процессы, связанные с диффузией.

§ 5.1. Феноменологическая теория  диффузии

Уравнения диффузии (первый и второй законы Фика). Если градиент концентрации одного из компонентов направлен по оси х, то поток этого компонента направлен в сторону уменьшения градиента концентрации и равен

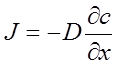                                               (5.1)

Отношение 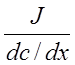=-D называют коэффициентом диффузии.

Уравнение (5.1) – первый закон Фика – неудобно для практического использования. Более удобным оказывается другое дифференциальное уравнение, которое можно получить из уравнения (5.1) и из условия, что концентрация в рассматриваемом объеме изменяется во времени (условие баланса вещества). В окончательном виде это уравнение - второй закон Фика имеет вид

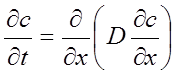                                          (5.2)

Для трех измерений уравнение (5.2) запишем в виде dc/dt = -divJ. Это уравнение выражает закон сохранения вещества в форме уравнения непрерывности и остается справедливым и в тех случаях, когда уравнением (5.1) пользоваться нельзя (например, при наличии добавочных градиентов, кроме концентрационного).

Коэффициент диффузии – это параметр, характеризующий скорость диффузии. С увеличением температуры для металлов коэффициент диффузии резко возрастает, изменяясь по экспоненциальному закону:

D(T)=D₀exp(-Q/RT).                                            (5.3)

где D₀ - предэкспоненциальный или частотный множитель;

Q - энергия активации;

R - газовая. постоянная;

Т - абсолютная температура.

Q и D₀ связаны с физико-химическими свойствами металла, а также диффундирующих частиц;

Экспоненциальный характер изменения коэффициента диффузии в зависимости от температуры был установлен эмпирически (закон Аррениуса), а затем обоснован теоретически.

Размерность коэффициента диффузии можно определить из уравнения (5.1). Обычно используют размерность сантиметр квадратный на секунду [см²/с], которая означает, что 1 моль вещества проходит сквозь площадку в 1 см² за 1 с при градиенте концентрации дс/дх, равном молю на сантиметр. Иногда коэффициенты диффузии относят не к секунде, а к суткам. В этом случае размерность имеет вид [см²/сут]. Значения констант, входящих в уравнение (5.3) для некоторых диффузионных пар, приведены в таблице 5.1.

В практике физических исследований обычно встречаются две группы диффузионных задач. В первой из них неизвестны коэффициент диффузии D, а также предэкспоненциальный множитель D₀ и энергия активации Q. Требуется их определить из известных диффузионных характеристик. Во второй группе задач по заранее известному коэффициенту диффузии необходимо определить те или иные диффузионные характеристики: распределение концентрации диффундирующего вещества, поток вещества через какую либо поверхность, количество вещества, проникшего в материал за известное время или же вышедшее из него.

Для решения указанных диффузионных задач необходимо знать аналитические зависимости между диффузионными характеристиками в интегральном виде. Эти зависимости могут быть получены интегрированием основного уравнения (5.2) при соответствующем выборе начальных и граничных условий, характеризующих конкретные физические условия рассматриваемой задачи.

Примеры решения основного уравнения диффузии. Предположим, что начальное распределение концентрации в теле задано в виде

c(x,0)=f(x)  (5.4)

и коэффициент диффузии не зависит от концентрации.

Таблица 5.1

Константы диффузии, входящие в уравнениеD=D₀exp(-Q/RT)