Опытные исследования гидродинамики, теплообмена в режимах однофазной конвекции и кипения, колебаний температур в предкризисных и кризисных режимах кипения, страница 12

Начальное условие:

Граничные условия:

где a(j) – локальный коэффициент теплоотдачи. Мишень нагревается только с верхней стороны, боковые и нижняя стороны являются адиабатными.

Описание процедуры численного решения прямой краевой задачи теплопроводности содержится в [155, 130]. Для расчета коэффициента теплоотдачи при однофазной конвекции и пузырьковом кипении, определения температурной границы смены режимов теплообмена, использовались собственные методики [156–160], представленные далее. Исходными данными для работы программы, реализующей численное решение задачи теплопроводности, являлись среднемассовая температура, массовая скорость и давление жидкости в сечении расположения термопар и плотность подводимого теплового потока, определяемые из экспериментальных данных. Выходными данными при достижении стационарного распределения температур являлись температурное поле мишени и распределение коэффициента теплоотдачи, температуры и плотности отводимого теплового потока по внутреннему периметру канала.

Сравнение результатов обработки двумя описанными способами представлено для данных, полученных на рабочем участке №2 на рис. 2.20 в виде зависимости плотности теплового потока в лобовой точке от температурного напора. Темными маркерами показаны результаты, полученные градиентным методом, светлыми – решением краевой задачи теплопроводности. Для конвективной области и начала кипения (DT < 230 K) наблюдается вполне удовлетворительное согласование обоих методик, что говорит о возможности применения градиентного метода для обработки данных. Расхождение в области развитого пузырькового кипения (DT > 230 K) показывает неприменимость градиентного метода для данных рабочего участка № 2 в области относительно высоких тепловых нагрузок.

Первичные опытные данные для рабочего участка №3 были обработаны с использованием только численного решения краевой задачи теплопроводности. Критерием достоверности полученных результатов являлось соответствие расчетных и измеренных температур мишени для РУ №2 и №3. На рис. 2.21 для одного из режимов показано типичное сравнение расчетных и измеренных температур для РУ №2. Как видно из данного сравнения, различие между расчетными значениями температур и измеренными не превышает погрешность измерения температуры, что свидетельствует о надежности получаемых расчетных данных.

Рис. 2.20. Зависимость плотности теплового потока от температурного напора в лобовой точке: темные маркеры – градиентный метод, светлые – решение краевой задачи теплопроводности; РУ №2, rw= 4500 кг/(м²×с), k = 0,37, p = 1,0 МПа, T_ж = 20 °C

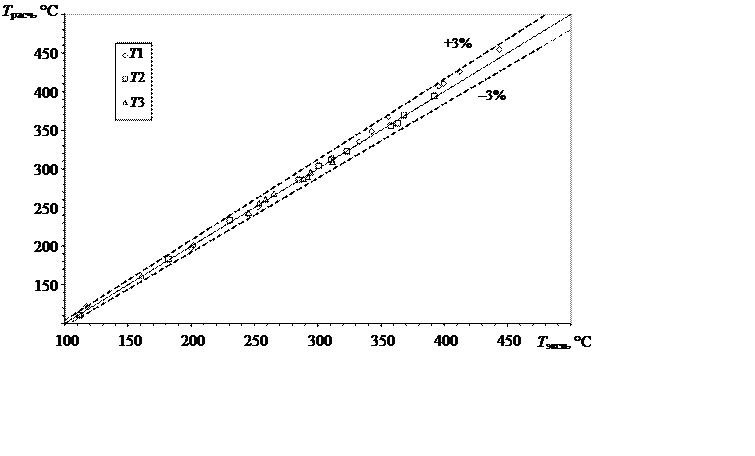
Рис. 2.21. Сравнение температур, измеренных в эксперименте термопарами и полученных методом решения краевой задачи теплопроводности в точках размещения термопар для РУ №2 при режимных параметрах: rw = 4500 кг/(м²×с), k = 0,37, p = 1,0 МПа и T_ж = 20 °C

Для проверки корректности получаемых расчетных данных для РУ №3 дополнительно использовался следующий метод. Варьируя плотность подводимого теплового потока, добивались соответствия в пределах погрешности измерений расчетных и измеренных значений температуры мишени в месте расположения термопары Т3 (рис. 2.9), сравнивая при этом задаваемое значение плотности теплового потока и определяемое из эксперимента. Результаты данного сравнения для одного из режимов показаны на рис. 2.22 в виде зависимости плотности подводимого теплового потока от подводимой мощности. Сравнение измеренных и расчетных значений температур для РУ №3 показано на рис. 2.23.

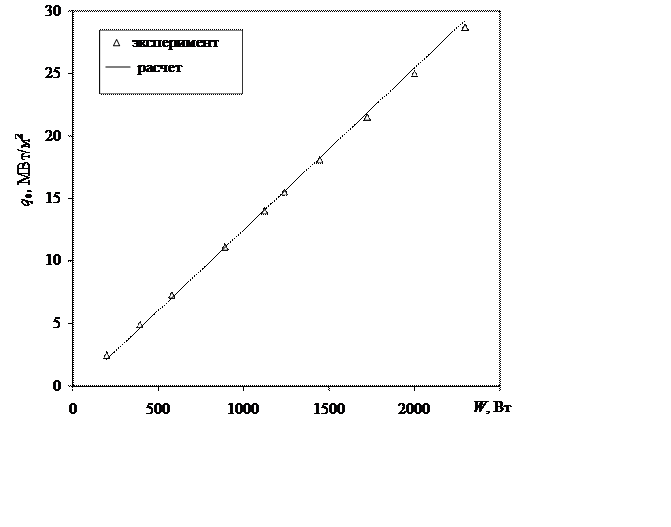
Рис 2.22. Зависимость плотности теплового потока от подводимой мощности для РУ №3 при ρw=9550 кг/(м²∙с) и p=0,7 МПа, труба без ленты.

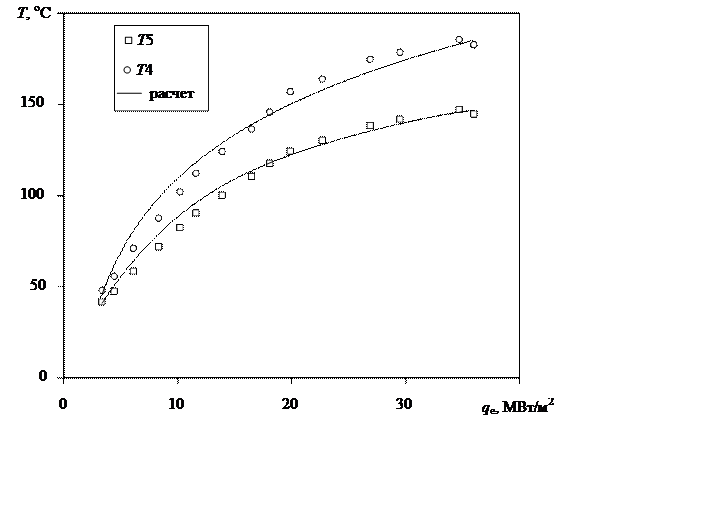
Рис 2.23. Сравнение измеренных и рассчитанных температур для РУ №3 при ρw=15900 кг/(м²∙с) и p= 0,8 МПа, труба без ленты