Опытные исследования гидродинамики, теплообмена в режимах однофазной конвекции и кипения, колебаний температур в предкризисных и кризисных режимах кипения, страница 11

Рис. 2.15. Зависимость плотности теплового потока от силы анодного тока

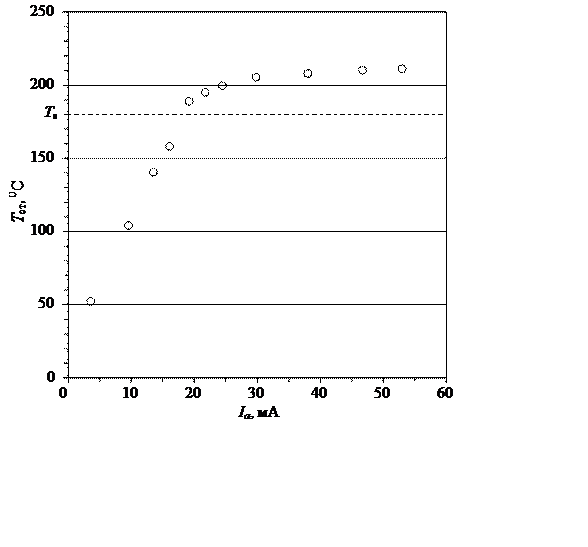
Рис. 2.16. Зависимость температуры стенки канала в лобовой точке от силы анодного тока

Надежность использования линейной зависимости температуры от радиуса подтверждает рис. 2.17, на котором представлены измеренные температуры в мишени рабочего участка № 1 при фиксированной тепловой нагрузке на тепловоспринимающей поверхности q_e и следующих параметрах потока воды: p = 1.0 МПа, Т_ж = 20 ^оC, k = 0,66 при различной массовой скорости. Сравнение плотности теплового потока для данных рис. 2.17 представлено в табл. 2.4, в которой плотность подводимого теплового потока q_e,э рассчитывалась по измерениям анодного тока, а плотность теплового потока q_i,0 в лобовой точке внутреннего периметра определялась по измеренному распределению температур. Данные табл. 2.4 показывают хорошее соответствие измеренной плотности теплового потока с результатами расчета, выполненными по температурному полю.

Рис. 2.17. Измеренное температурное поле в поперечном сечении мишени рабочего участка №1

Таблица 2.4. Сравнение плотности теплового потока

Результаты температурных измерений на рабочем участке №2 аналогичны данным для участка №1. На рис. 2.18 представлено измеренное термопарами Т1–Т3 (см. рис.2.8) распределение температур от координаты заделки термопар при теплообмене в режиме однофазной конвекции. Как видно из рис. 2.18, при умеренных тепловых нагрузках распределение температуры по оси симметрии мишени также линейно. Результаты определения плотности теплового потока и температуры стенки по результатам линейной аппроксимации отображены на рис. 2.18.

При использовании линейной аппроксимации температуры определяемая по градиенту температуры плотность теплового потока одинакова на внутренней и внешней поверхности с точностью учета зависимости теплопроводности материала от температуры. Критерием надежности получаемых результатов при аппроксимации полученного характерного распределения температур с последующей экстраполяцией на стенку является соответствие плотности теплового потока, определенной по градиенту температур и измеренной подводимой. Подобное сравнение, выполненное по всему массиву данных о конвективном теплообмене, полученных на участках № 1 и 2, представлено на рис. 2.19. Данные на участке № 1 получены при трех фиксированных значениях силы анодного тока и соответственно плотностях теплового потока q_е» 2, 3 и 4.5 МВт/м². Сравнение показывает хорошее соответствие плотностей теплового потока. Согласно выполненным оценкам погрешность определения плотности теплового потока по данной методике не превышает 8%, коэффициента теплоотдачи - 10% [156].

Рис. 2.18. Расчет температуры и плотности теплового потока в лобовой точке методом линейной экстраполяции для рабочего участка №2 при         rw=4500 кг/(м²×с), k = 0,37, T_вх = 20 °C, p = 1,0 МПа

Рис. 2.19. Сравнение измеренной плотности теплового потока q_e,э и полученной из распределения температур q_i,o

С увеличением тепловой нагрузки на стенке канала начинается кипение, неизотермичность внутреннего периметра канала увеличивается. При относительно высоких тепловых нагрузках распределение температуры по оси симметрии мишени становится нелинейным. В этом случае использование градиентного способа для данных рабочего участка № 2 приводит к неверному определению плотности теплового потока. Температуры на внутренней поверхности и плотности теплового потока при относительно высоких тепловых нагрузках (как правило соответствующих развитому кипению на стенке) для рабочего участка № 2 определялись из численного решение прямой двухмерной краевой задачи теплопроводности в мишени рабочего участка со следующими граничными условиями: