
Задание 8.
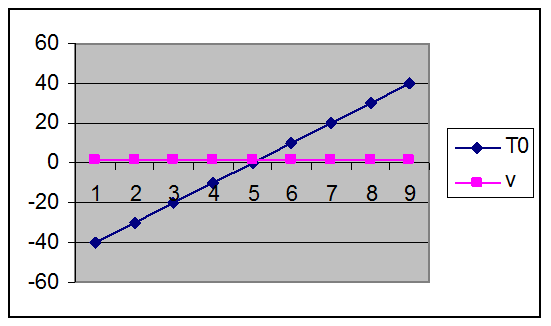
Подсчитать для Т0 = 0°С величины (nw)t*+0/nw2 и (nw)t**+0/nw3. Для первой из этих величин построить график зависимости от Т0 в интервале -40< T0 <+40°C. Использовать данные таблицы.
Исходные данные для расчёта:
|
№ варианта |
n |
В, °С |
Ts, °С |
P1 |
P2 |
P3 |
|
1 |
0.4 |
450 |
300 |
20 |
50 |
30 |
Решение:
Требуется найти отношения, характеризующие степень нестационарности
Vw(t*+0)/vw2, Vw(t**+0)/vw3,если для стационарной скорости горения известны А, В, v в (1) и (2).
vw = v1(P/ 1 атм)n, n < 1. (1)
v1 = A/ (B – T0). (2)
j(t* + 0) = j1
(vw)t*+0 = vw(P2,j1). (3)
j = vst(P, ![]() ) (Ts –
) (Ts –![]() )/k. (4)
)/k. (4)
vw(P, j) = vst (P, ![]() (P, j)).
(5)
(P, j)).
(5)
Чтобы получить конкретный вид выражений (4) и (5), подставим (1) и (2) в уравнение (5):
vst(P, Т0*) = A(P/1 атм)n/(B – T0*),
j = vst(P, Т0*) (Ts – T0*)/k,
откуда следует
B – T0* = A(P/1 атм)n/vst(P, Т0*),
Ts–T0* = kj/vst(P, Т0*),
после чего совместное решение этих уравнений приводит к исключению Т0*. Тогда с использованием уравнения (5) получаем
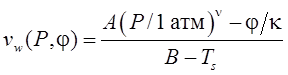 .
(6)
.
(6)
Здесь В > Ts. Теперь можно найти искомое отношение
(vw)t*+0/vw2 = vw (P2, j1)/vw2 = 1 + [1 – (P1/P2)n] (Ts – T0)/(B– Ts). (7)
По аналогии
j(t** + 0) = j2
(vw)t**+0 = vw(P3, j2)
(vw)t**+0/vw3 = vw (P3, j2)/vw3 = 1 + [1 – (P2/P3)n] (Ts – T0)/(B– Ts). (8)
(vw)t*+0/vw2 = 1+[1 – (P1/P2)n] (Ts – T0)/(B– Ts).
(vw)t**+0/vw3 = 1 + [1 – (P2/P3)n] (Ts – T0)/(B – Ts)
(vw)t*+0/vw2 (T0 = 0)= 1+ ((1-СТЕПЕНЬ((20/50);0,4))*((300-0)/(450-300))) = 1,613
(vw)t**+0/vw3 (T0 = 0)=1+ ((1-СТЕПЕНЬ((50/30);0,4))*((300-0)/(450-300)))=0,546
|
T0 |
v |
|
-40 |
1,695 |
|
-30 |
1,675 |
|
-20 |
1,654 |
|
-10 |
1,634 |
|
0 |
1,613 |
|
10 |
1,593 |
|
20 |
1,572 |
|
30 |
1,552 |
|
40 |
1,531 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.