Определение ускорения свободного падения при помощи оборотного и математического маятников. Вариант 3

является кратным 10 мм, а фиксирующие воротки размещены так, чтобы при помощи кольцевых углублений их можно было бы фиксировать в нужном положении.

Нижний кронштейн 5 вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки 3 и фиксировать в произвольно выбранном положении.

Расчетные формулы:

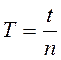                                                                                                                                                 (1)

где         t – измеренное время,

n – число колебаний,

T – период колебаний.

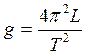                                                                                                                                                    (2)

где         g – ускорение свободного падения,

T – период колебаний,

L(для математического маятника) – расстояние от конца оборотного маятника до опорной призмы ,

L(для оборотного маятника) - расстояние между опорными призмами.

Формулы для расчёта погрешностей.

(3) 

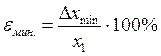
где         ε_мин. – минимальная относительная погрешность прямых измерений;

Dx_min – абсолютная минимальная погрешность прямых измерений;

x₁ –результат первого наблюдения.

(4) 

где         Dx_min – абсолютная минимальная погрешность прямых измерений;

Dx_приб. – приборная погрешность;

Dx_округ. – погрешность округлений.

(5) 

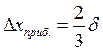
где         Dx_приб. – приборная погрешность;

δ – предельная приборная погрешность (равняется 1см – для линейки в опыте №1 и 1 мм – в опыте №2, 1*10^-4 с – для миллисекундомера).

(6) 

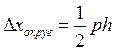
где         Dx_округ. – погрешность округлений;

p = 0,95 – доверительная вероятность;

h – интервал округления (равняется 1см – для линейки в опыте №1 и 1 мм – в опыте №2, 1*10^-4 с – для миллисекундомера).

(7) 

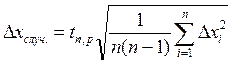
где         Dx_случ. – случайная погрешность прямых измерений;

t_n,p = 2,26 – коэффициент Стьюдента, при n=10 и p=0,95;

n – количечтво экспериментов;

Dx_i – отклонение данного результата от среднего ().

(8) 

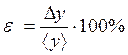
где         ε – относительная погрешность косвенных измерений;

Dy – абсолютная погрешность косвенных измерений;

<y> – среднее значение результатов наблюдения.

(9) 

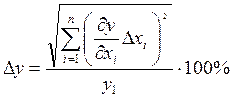
где         Dy – абсолютная погрешность косвенных измерений;

 – абсолютная погрешность прямых измерений;

y₁ – результаты первого наблюдения.

После подстановки соответствующих значений x и y получили следующие формулы для определения минимальной и полной погрешностей измерения величины g:

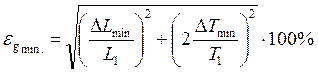                                                                                                                                    (10)

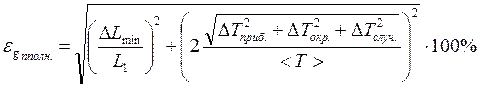                                                                                                                                                   (11)

Формулы для расчета величин по методу наименьших квадратов:

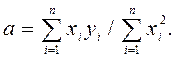                                                                                                                                                   (12)

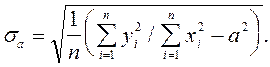                                                                                                                                                   (13)

Da_c = 3s_a                                                                                                                                                                                                                                                     (14)

e_a,c = Da_c/a 100 %.                                                                                                                                               (15)

В нашем случае принимаем, что y = L,  x = T²/4p и соответственно в результате получаем  a = g.

Предварительная оценка погрешностей.

Опыт 1:

а)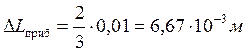

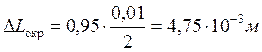
L = 0,32 м

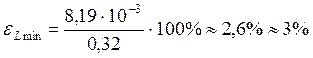
б)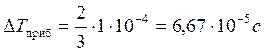

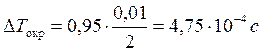
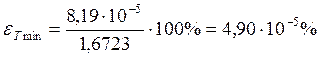
в)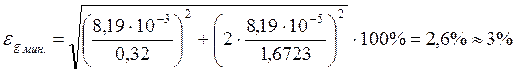

Опыт 2:

а)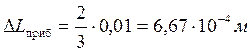 

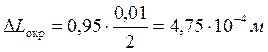
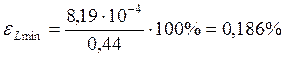
б)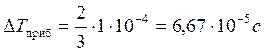

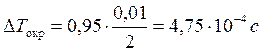
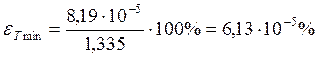
в)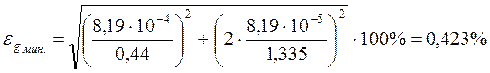

Выполнение работы:

Опыт 1:

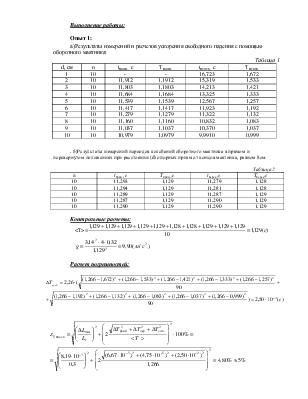
а)Результаты измерений и расчетов ускорения свободного падения с помощью оборотного маятника:

Таблица 1

d, см	n	tпрям., с	Tпрям.	tперев., с	Tперев.
1	10	-	-	16,723	1,672
2	10	11,912	1,1912	15,319	1,533
3	10	11,803	1,1803	14,213	1,421
4	10	11,684	1,1684	13,325	1,333
5	10	11,539	1,1539	12,567	1,257
6	10	11,417	1,1417	11,923	1,192
7	10	11,279	1,1279	11,322	1,132
8	10	11,160	1,1160	10,832	1,083
9	10	11,037	1,1037	10,370	1,037
10	10	10,979	1,0979	9,9910	0,999

. б)Результаты измерений периодов колебаний оборотного маятника в прямом и перевернутом положениях при расстоянии (d) опорных призм от концов маятника, равном 8см.

Таблица 2

n	tпрям.,с	Tпрям.,с	tперев.,с	Tперев,с
10	11,293	1,129	11,279	1,128
10	11,294	1,129	11,281	1,128
10	11,289	1,129	11,287	1,129
10	11,287	1,129	11,290	1,129
10	11,290	1,129	11,290	1,129

Контрольные расчеты:

<T>=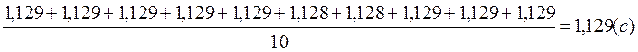

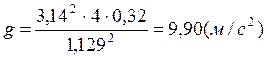
Расчет погрешностей:

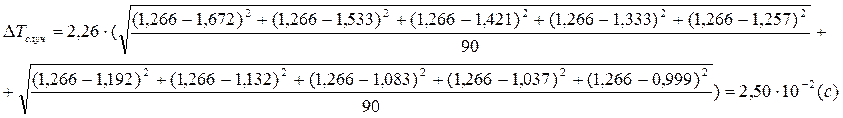
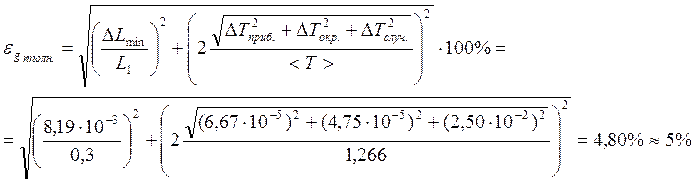
Опыт 2:

Результаты измерений и расчетов ускорения свободного падения с помощью математического маятника:

Таблица 3

n	1	2	3	4	5	6	7	8	9	10
L, м	0,44	0,43	0,42	0,41	0,40	0,39	0,38	0,37	0,36	0,35
t, с	13,35	13,19	13,06	13,01	12,79	12,60	12,39	12,28	12,22	12,02
T, с	1,34	1,32	1,31	1,30	1,28	1,26	1,24	1,23	1,22	1,20
T2, с2	1,78	1,74	1,70	1,69	1,64	1,59	1,54	1,51	1,49	1,44
g, м/с2	9,73	9,75	9,72	9,55	9,64	9,69	9,76	9,67	9,51	9,56

Контрольные расчеты:

                         

                         

                         

                         

                                                                                                                      

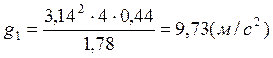
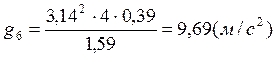
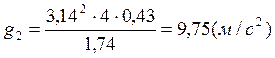
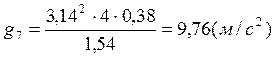
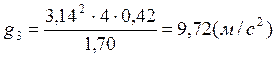
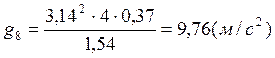
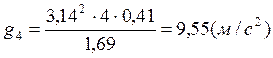
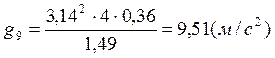
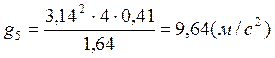
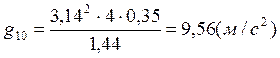
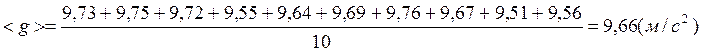
Расчет ускорения свободного падения с использованием метода наименьших квадратов:

Таблица 4

N
1	0,045	0,44	0,0198	0,00203	0,194
2	0,044	0,43	0,0189	0,00194	0,185
3	0,043	0,42	0,0181	0,00185	0,176
4	0,043	0,41	0,0176	0,00185	0,168
5	0,041	0,40	0,0164	0,00168	0,160
6	0,040	0,39	0,0156	0,00160	0,152
7	0,039	0,38	0,0148	0,00152	0,144
8	0,038	0,37	0,0141	0,00144	0,137
9	0,038	0,36	0,0137	0,00144	0,130
10	0,037	0,35	0,0130	0,00137	0,123
Сумма	0,408	3,95	0,1619	0,01672	1,569

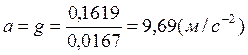
Оценка погрешности по  методу наименьших квадратов:

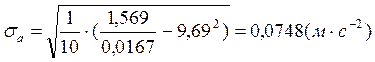
_с=0,0748∙3=0,223(м∙с^-2)

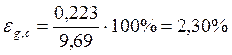
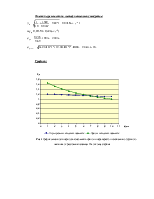
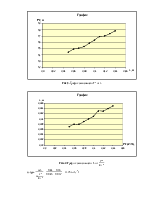
Графики:

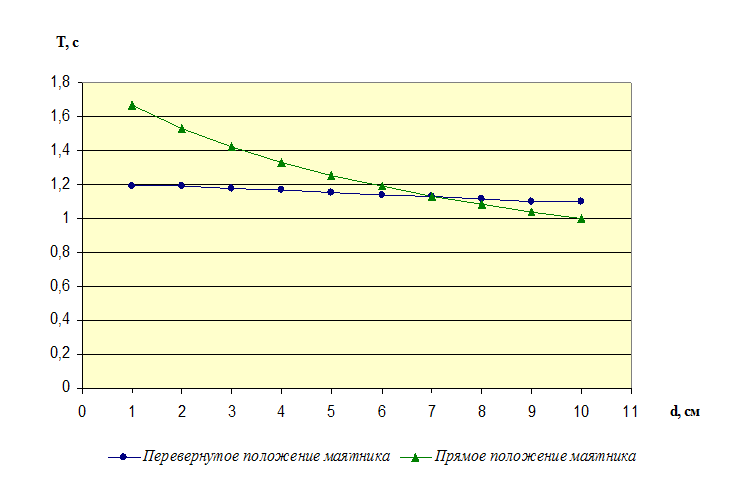
Рис 2 График зависимости периодов колебаний в прямом и перевернутом положениях оборотного маятника от расстояния чечевицы 12а от конца стержня

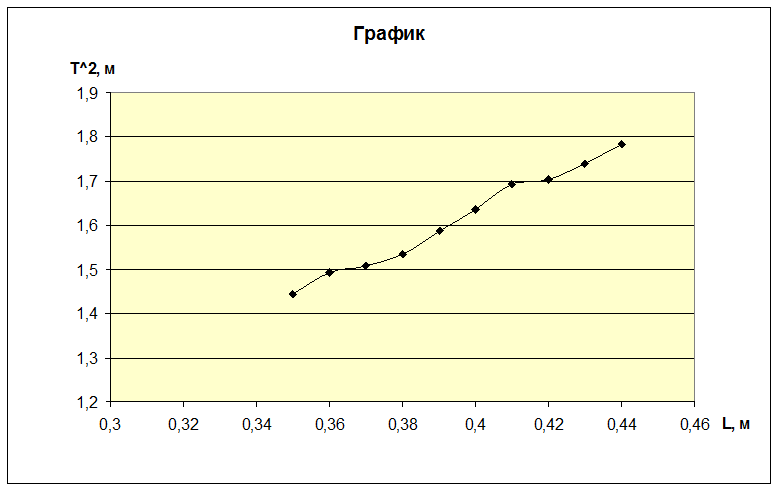
Рис.3. График зависимости T² от L.

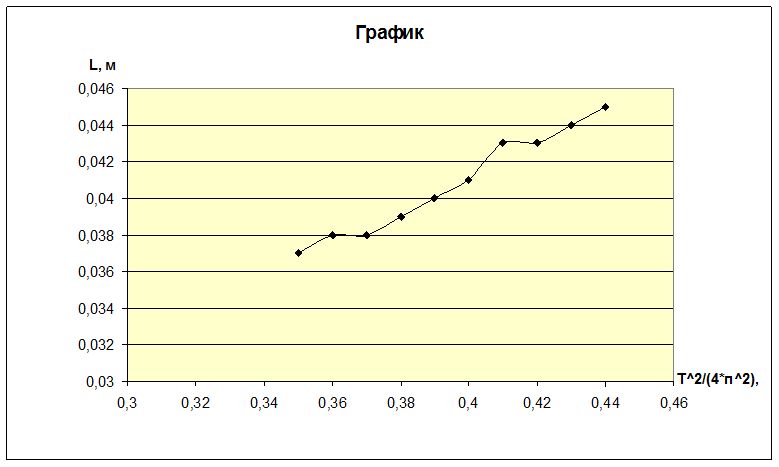
Рис.4 График зависимости L от

g=tgα=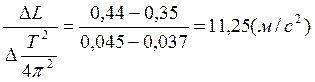

Окончательный результат  измерений

1)Для физического маятника:

м/с², при р = 0,95.

2)Для математического маятника:

м/с², при р = 0,95.

Вывод: В ходе выполнения лабораторной работы путем эксперимента на примере обратного и математического маятника определили ускорение свободного падения.

В первом опыте было необходимо, изменяя момент инерции (передвигая чечевицу), добиться того, чтобы расстояние между опорными призмами стало равным приведенной длине оборотного маятника. Для этого построили график зависимости периодов колебания в прямом и перевернутом положении от расстояния чечевицы от конца стержня. Точка пересечения данных графиков соответствовала равенству периодов этих колебания и соответственно была равно приведенной длине. В нашем случае данная точка соответствовала L=7. Повторили опыты для данного расстояния. По полученным результатам вычислили Т, а затем и g.

Во втором опыте проводили схожие измерения, но для математического маятника. Измерили t для n=10 при различной длине. Вычислили период колебания. Далее при помощи метода наименьших квадратов оценили <g> и случайную относительную погрешность. Метод наименьших квадратов использовался для получения более точных