Определенный интеграл. Определение и основные свойства определенного интеграла. Несобственные интегралы II рода (от неограниченных функций)

3. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

3.1. Определение и основные свойства определенного интеграла

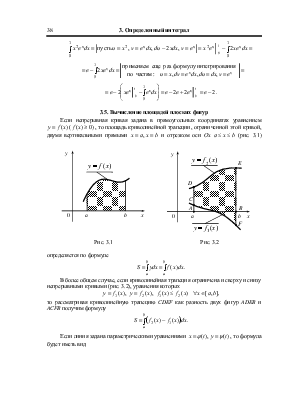
Пусть функция  определена на отрезке . Разобьем этот отрезок на        частей точками  .

На каждом из частичных отрезков  возьмем произвольную точку  и составим сумму

  , которая называется интегральной суммой функции  на отрезке .

Предел интегральной суммы при условии, что число частичных отрезков неограниченно увеличивается, а длина наибольшего из них стремиться к нулю, называется определенным интегралом функции  в пределах от  до  и обозначается

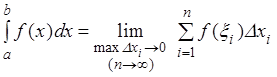                                           (3.1)

Если функция непрерывна на отрезке , то она интегрируема на этом отрезке, т.е. предел (3.1) существует и не зависит от способа разбиения промежутка интегрирования  на частичные отрезки и от выбора точек  при каждом таком разбиении.

Основные свойства определенного интеграла

1^о. .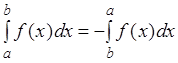

2^о.

где  и  – постоянные.

3^о. ,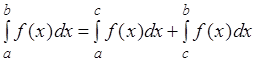

где  – некоторая точка, лежащая внутри или вне отрезка .

3.2. Формула Ньютона-Лейбница

Если функция  непрерывна на отрезке  и для нее известен неопределенный интеграл , где  – какая либо первообразная функции , то определенный интеграл может быть вычислен по формуле Ньютона-Лейбница

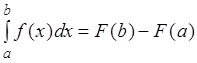,                                                 (3.2)

т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

При вычислениях формулу (3.2) обычно записывают в виде

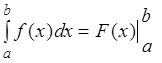, где символ в правой части равенства – "подстановка от  до " – обозначает ту же самую разность .

Пример 3.1.  Вычислить интеграл  .

Решение.

.

3.3. Замена переменной в определенном интеграле

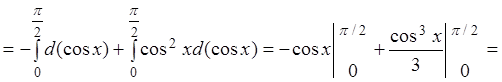
Часто для вычисления интеграла 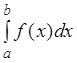 полезно заменить переменную интегрирования  новой переменной  при помощи подстановки  или . При этом необходимо перейти от старых пределов интегрирования  и  к новым пределам  и  которые определяют из уравнений ,  или

Замена переменной осуществляется по формуле

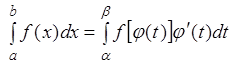                                            (3.3)

Эта формула справедлива, если  – непрерывная функция, а функция  сама непрерывна и имеет непрерывную производную на отрезке .

При вычислении определенного интеграла методом замены переменной возврат к старой переменной не требуется.

Пример 3.2. Вычислить интеграл  .

Решение. Положим , тогда . Такая подстановка возможна (так как при любом значении  под корнем получается неотрицательная величина) и приводит к тому, что корень под знаком интеграла исчезает. При этом изменению переменной  от  до  соответствует изменение переменной   от  до . Применяя формулу (3.3) получаем

.

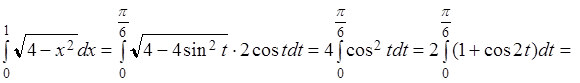
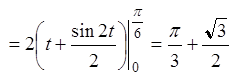Пример 3.3.  Вычислить интеграл .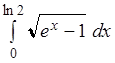

Решение. Положим , тогда e^x – 1 = t², e^x = t² + 1, дифференцируем обе части равенства: e^xdx = 2tdt, откуда .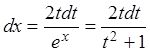 

При                             x = 0: ;

при                                    x = ln2: , поэтому

3.4. Интегрирование по частям в определенном интеграле

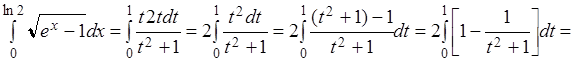
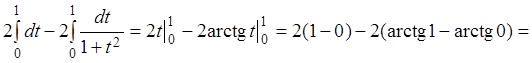
Если функции  v(x)  и  u(x)обладают непрерывными производными на отрезке   [a, b], то справедлива формула интегрирования по частям для определенного интеграла

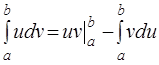                                                       (3.4)

Пример 3.4. Вычислить интеграл  .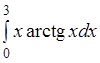

Решение.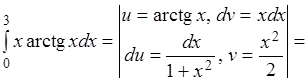

.

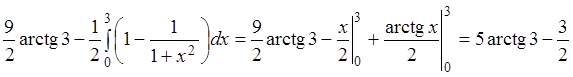Пример 3.5. Вычислить интеграл  .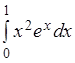

Решение.

.

3.5. Вычисление площадей плоских фигур

Если непрерывная кривая задана в прямоугольных координатах уравнением , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикальными прямыми  и отрезком оси Оx  (рис. 3.1) определяется по формуле

.

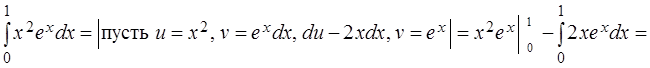
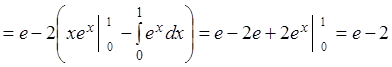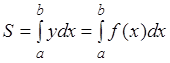В более общем случае, если криволинейная трапеция ограничена и сверху и снизу непрерывными кривыми (рис. 3.2), уравнения которых

, то рассматривая криволинейную трапецию CDEF как разность двух фигур ADEB и ACFB получим формулу

.

Если линия задана параметрическими уравнениями , то формула будет иметь вид

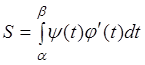, где  – значения, между которыми изменяется параметр t, когда точка пробегает слева направо всю линию, ограничивающую трапецию сверху.

Пусть дан сектор OAB, ограниченный дугой АВ и двумя радиус-векторами ОА и ОВ (рис. 3.3). При этом дуга АВ задана в полярной системе координат уравнением , где  – положительная, непрерывная на отрезке  функция. Тогда площадь сектора АОВ вычисляется по формуле

.

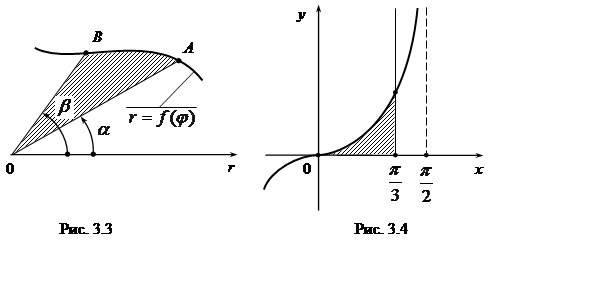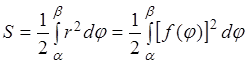Пример 3.6. Вычислить площадь фигуры, заключенной между кривой , осью Ox и прямой .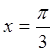

Решение. Построим данную криволинейную трапецию (рис. 3.4) и вычислим ее площадь

.

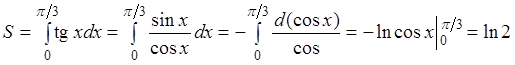Пример 3.7. Вычислить площадь фигуры, ограниченной параболами .

Решение. Решая систему уравнений

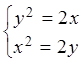 , находим абсциссы точек пересечения парабол  и значит

.

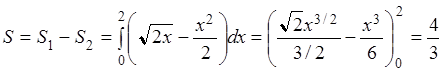Пример 3.8. Вычислить площадь эллипса .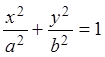

Решение. Здесь удобнее записать параметрические уравнения эллипса, которые