Неизотермический реактор периодического действия

63 вопрос

Неизотермический реактор периодического действия

Поддержание постоянной температуры является достаточно сложной технической проблемой. Кроме того, в ряде случаев по технологическим соображениям необходимо поддерживать переменную температуру в реакторе. Рассмотрим работу неизотермического реактора, в котором протекает единственная реакция первого порядка

,         .                                      (5.34)

В данном случае необходимо совместное рассмотрение уравнений баланса массы и энергии, например (5.8) и (5.9).

Учтем, что в данном случае и, следовательно, в соответствии с (2.5) , константа скорости реакции определяется законом Аррениуса (3.23),где опорная температура  - температура теплоносителя в теплообменнике, начальные условия (для t = 0) определяются некоторыми значениями  и  (температура в реакторе). При рассмотренных условиях систему уравнений, описывающую реактор, можно представить в виде

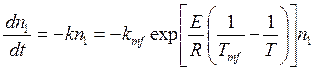;                         (5.35)

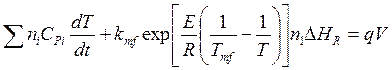;            (5.36)

;                                                    (5.37)

:  ,         .                                       (5.38)

Здесь  - общая площадь теплообменной поверхности в объеме V,  - коэффициент теплопередачи теплоноситель/реакционная среда.

Переход к безразмерным переменным. Уравнения (5.35) - (5.38) содержат достаточно большое число параметров: , , , , , , , , , , , . Это затрудняет анализ уравнений и описываемых ими закономерностей. Существенное сокращение числа параметров может быть достигнуто на основе перехода к безразмерным переменным. При этом размерные параметры группируются в безразмерные комплексы, число которых значительно меньше, чем размерных. Оценить минимальное число безразмерных комплексов можно на основе анализа размерностей. Основная теорема теории размерностей (-теорема) гласит, что если уравнения содержат n размерных величин и m основных размерностей, то минимальное число безразмерных комплексов при переходе к безразмерным координатам равно N = n - m. Данное утверждение является следствием постулата о том, что физический закон не зависит от применяемой системы единиц. Пусть имеем некоторый набор параметров р₁, р₂, р₃, р₄,... и три основных размерности, например, грамм, метр, секунда, сделаем переход к другим единицам измерения, домножив каждую из размерностей на некие коэффициенты k₁, k₂, k₃. Так как k₁, k₂, k₃ - произвольные, то можно потребовать, чтобы эти коэффициенты были такими, чтобы три параметра в новой размерности

    (i = 1, 2, 3).                     (5.39)

Система из трех уравнений (5.39) может быть действительно решена относительно трех коэффициентов k_i. Следовательно, при переходе к новым масштабам размерностей мы будем иметь новый набор параметров  1, 1, 1, , , т. е. число параметров уменьшилось на 3.

Возвращаясь к системе уравнений (5.35) - (5.38), поступим следующим образом. Введем безразмерные переменные

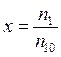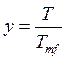,         ,        .                           (5.40)

Заменяя в (5.35) - (5.38) переменные n₁, T, t на новые, получим

;                                 (5.41)

;                    (5.42)

: , .                                  (5.43)

Число параметров в (5.41) - (5.43) уменьшилось до четырех.

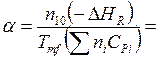 (если V = const) 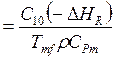;              (5.44)

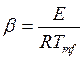;                                            (5.45)

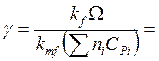 (если V = const) 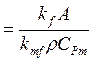;                  (5.46)

.                                          (5.47)

где ; ;  - плотность;  - удельная теплоемкость смеси.

Решая систему (5.41) - (5.43) численно, можно проанализировать влияние безразмерных параметров , ,  на зависимость изменения безразмерных характеристик х и у от безразмерного времени . Реальные диапазоны изменения размерных параметров находятся в следующих пределах:  1/с,  кмоль/м³,  кДж/моль,  Дж/(м³К),  К,  Bт/(м²K),  м²/м³,  кДж/моль,  Дж/(моль К). При этом диапазоны изменения безразмерных параметров следующие: , , .

На рисунке 5.2 показаны зависимости  и  для постоянных  и , но различных . Из рисунка видно, что в зависимости от  возможны два режима работы реактора: (1) неустойчивый (малые  - большая неизотермичность), (2) устойчивый (>5, - относительно малые разогревы). В первом случае неконтролируемый разогрев может привести к появлению побочных реакций, во втором - процесс может быть осуществлен в необходимом интервале температур в обозримое время. Вопрос тепловой устойчивости является одним из наиболее важных при разработке реакторов.

 

Тепловая неустойчивость (реактор периодического действия)

Рассмотрим вопрос о тепловой неустойчивости на примере реакции  нулевого порядка (). В этом случае вместо (5.35) - (5.38) имеем

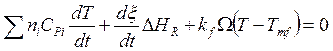;                      (5.48)

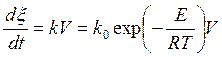,                                         (5.49)

где  - площадь поверхности теплообмена на единицу объема реактора.

Пусть имеет место экзотермическая реакция (). В случае  (условие постоянства или экстремума температуры при ) из (5.49) и (5.48)

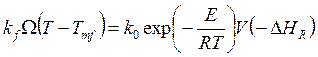 или ,               (5.50)

где

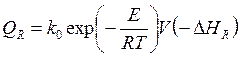;   .                  (5.51)

Уравнение (5.50) отражает баланс тепла реакции (Q_R) и отводимого теплообменником (Q_E).

На рис. 5.3 точки S и I - состояния, при которых (5.50) выполняется. Точка I соответствует неустойчивой ситуации. Действительно, любое отклонение от  будет приводить к дальнейшему самопроизвольному изменению температуры:

- при   - возрастает; это ведет к дальнейшему увеличению Т и еще большему увеличению (Q_R- Q_E) и т.д.;

- при   - уменьшается; это ведет к дальнейшему снижению т до тех пор, пока не будет достигнута точка .

Точка S соответствует устойчивому режиму. Действительно, при любом небольшом отклонении температуры Т от  возникает противодействие этому отклонению, а именно:

- при  ; это ведет к снижению т до тех пор, пока не будет достигнута температура .

- при  ; это ведет к увеличению т и снижению  до тех пор, пока не будет достигнута температура , при которой .

Точка С соответствует критическим параметрам теплообменника (величина  определяет наклон прямой  к оси абсцисс), при которых устойчивая работа реактора возможна и определяет максимально возможную разность температур , соответствующую устойчивой работе реактора.

В точке С одновременно должны выполняться условия (5.50) и условие равенства производных , т.е.

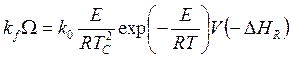.                             (5.52)

Из (5.50) и (5.52) для Т = Т_С можно получить

.                                                (5.53)

Из (5.53) при заданном T_mf определяется Т_С. С другой стороны при известной величине Т_С из (5.52) определяется критическое значение .

Рассмотренный пример показывает, что выбор параметров теплообменника  (k_f - коэффициент теплопередачи,  - общая площадь теплообменной поверхности в реакционном объеме) и разности температур Т - T_mf является очень ответственным моментом.

В случае неустойчивого режима работы предельный разогрев может быть порядка адиабатического (5.15), т.е.

.

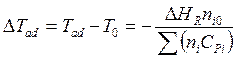Для реакторов полимеризации  составляет 400 - 1000°С.

В более общем случае, соответствующем реакции первого порядка (5.34), решая численно систему безразмерных уравнений (5.41) - (5.43), можно установить определенную область изменения безразмерных параметров (5.44) - (5.47), в которой процесс протекает устойчиво. На основе анализа решений для области  установлен полуэмпирический критерий стабильной работы периодического реактора

.                                                    (5.54)