








5 Однофазный реактор периодического действия (Batch Reactor) 44
5.1 Уравнения баланса массы и энергии. 44
5.2 Некоторые решения для изотермического реактора (T(t)= const) 48
5.2.1 Обратимая реакция второго порядка, dT/dt = 0, dV/dt = 0. 48
5.2.2 Две последовательные реакции 1-го порядка (dT/dt = 0) 49
5 Однофазный реактор периодического действия (Batch Reactor)
5.1 Уравнения баланса массы и энергии
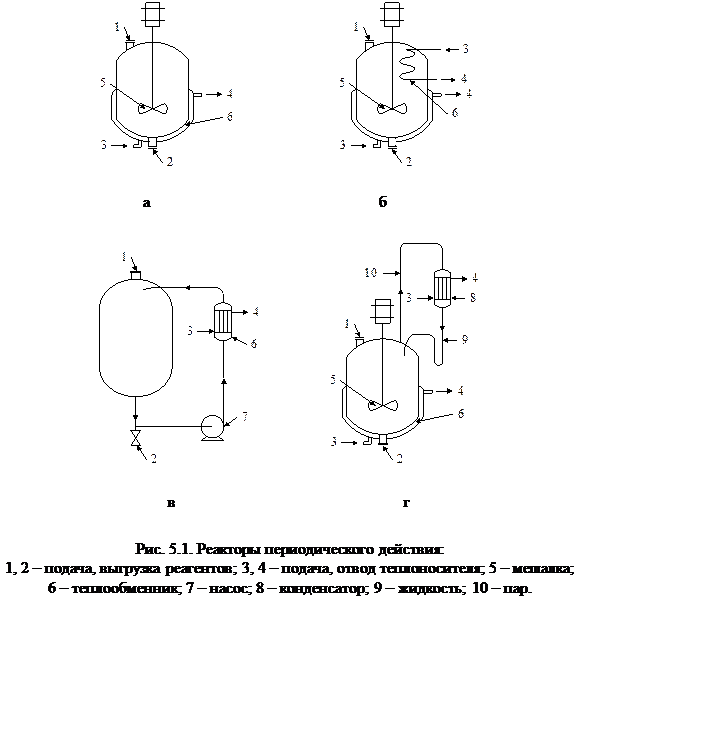
Схема реактора периодического действия показана на рисунке 5.1.
Цикл работы такого реактора включает стадии предварительной загрузки (1), выхода на режим по температуре и давлению (2), химического превращения (3), возврата к нормальным условиям (4), разгрузки (5) и механической очистки реактора от отложений на стенках и т.п. (6). Необходимая температура в реакторе может поддерживаться за счет циркуляции теплоносителя в охлаждающей рубашке (рис 5.1, а), за счет размещения в реакторе дополнительного теплообменника (рис 5.1, б), путем циркуляции реагентов через выносной теплообменник (рис 5.1, в), за счет испарения жидкости (в том числе и реагентов) в реакционном объеме и конденсации во встроенном или выносном конденсаторе с последующим возвратом конденсата в реакционный объем (рис 5.1, г). Обычно реакционная смесь в реакторе хорошо перемешивается так, что перемешивание можно считать идеальным. Химические превращения имеют место на стадиях (2) – (4).
Будем считать, что реакционная система характеризуется стехиометрическим уравнением (суммирование по повторяющимся индексам).
![]() ,
, ![]() , (
, (![]() ,
,![]() ,
,![]() - для инерта). (5.1)
- для инерта). (5.1)
Уравнения баланса массы и энергии для данного реактора легко получить, используя (4.1) – (4.11). Будем считать, что в период осуществления реакции в реактор не подаются и из реактора не выводятся реагенты (закрытая система) и в реакторе имеет место идеальное перемешивание.
Интегрируя, например, уравнение (4.10) по всему реакционному объему
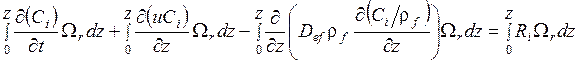 , (5.2)
, (5.2)
можно получить (с учетом, что в (5.2) третье слагаемое для случая идеального перемешивания равно нулю)
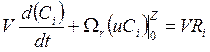 (i, … S) (5.3)
(i, … S) (5.3)
где z – верхняя граница реакционного
объема; ![]() - площадь поперечного сечения реактора, V=Z
- площадь поперечного сечения реактора, V=Z![]() - реакционный объем.
- реакционный объем.
Так как
в реактор реагенты не подаются и не выводятся, то ![]() ,
, ![]() (верхняя граница
(верхняя граница ![]() (жидкие
реагенты) движется только за счет расширения реакционного объема). При этом из
(5.3) имеем
(жидкие
реагенты) движется только за счет расширения реакционного объема). При этом из
(5.3) имеем
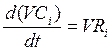 , (i, … S). (5.4)
, (i, … S). (5.4)
Уравнение (5.4) можно переписать в другом виде
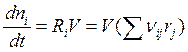 , (
, (![]() ), (
), (![]() ). (5.5)
). (5.5)
Аналогично можно получить из (4.2) и (4.11) соответственно
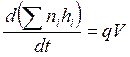 , (
, (![]() ), (5.6)
), (5.6)
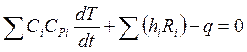 ,
, ![]() . (5.7)
. (5.7)
Уравнения (5.4), (5.6) можно представить в терминах химической
переменной ![]() , если учесть,
что
, если учесть,
что ![]() (см. (2.4),
(3.6)),
(см. (2.4),
(3.6)),
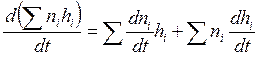 ,
, 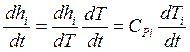
(![]() - определение
теплоемкости при постоянном давлении), и, следовательно,
- определение
теплоемкости при постоянном давлении), и, следовательно,
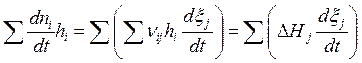 .
.
При этом можно получить
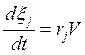 , (
, (![]() ); (5.8)
); (5.8)
![]() , (
, (![]() ), (
), (![]() ). (5.9)
). (5.9)
Первый член уравнения (5.9) связан с теплотой реакции, второй с изменением температуры реакционной среды, третий - с энергообменом с внешней средой.
С учетом (5.1) уравнения (5.4), (5.5), (5.8), так же, как и уравнения (5.6), (5.7), (5.9), эквивалентны.
Если реакция протекает без изменения объема смеси (см. п. 2.2), то из (5.5), (5.6) можно получить, разделив правые и левые части на V,
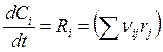 , (
, (![]() ), (
), (![]() ); (5.10)
); (5.10)
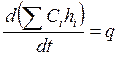 , (
, (![]() ). (5.11)
). (5.11)
Кроме теплообмена с внешней средой величина q может быть связана с диссипацией механической энергии потока, радиационным взаимодействием и другими эффектами, которые в дальнейшем учитываться не будут.
Чтобы проанализировать работу реактора, уравнения (5.8) и (5.9) необходимо решать совместно, задав начальные условия, например,
![]() :
: ![]() ,
, ![]() ,
, ![]() . (5.12)
. (5.12)
Наиболее простыми являются три частных случая, допускающие аналитические решения.
1.
Изохорический
процесс (![]() - реализуется,
если
- реализуется,
если ![]() , или
если реакционная среда - газ, или жидкая среда, но с малым содержанием реагентов).
, или
если реакционная среда - газ, или жидкая среда, но с малым содержанием реагентов).
2.
Изотермический
процесс (![]() или
или ![]() ).
).
3.
Адиабатический
процесс (![]() ).
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.