Однофазный реактор периодического действия (Batch Reactor), страница 2

Температура адиабатического разогрева реактора () – это температура разогрева реакционной среды (реактора) в отсутствии теплообмена с внешней средой в случае полного превращения реагентов. Если имеется только одна реакция , то (5.9) для адиабатического случая принимает вид

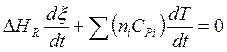 или ,                    (5.13)

откуда, если правая часть слабо зависит от Т и ,

.                                           (5.14)

В случае полного превращения и, следовательно,

.                                 (5.15)

5.2 Некоторые решения для изотермического реактора (T(t)= const)

В этом случае уравнение энергии исключается и решаются только уравнения баланса массы. Рассмотрим несколько типов реакций.

5.2.1 Обратимая реакция второго порядка, dT/dt = 0, dV/dt = 0

Пусть имеем одну обратимую реакцию второго порядка

.                                          (5.16)

Пусть (5.16) – это реакция 1-го порядка по каждому компоненту, общий порядок – 2-й. При этом в общем случае закон действующих масс может не соблюдаться и для реакции первого порядка по каждому компоненту стехиометрические коэффициенты мoгут быть отличными от .

В этом случае в соответствии с (3.11) скорость реакции (5.16)

,                                (5.17)

где ; ; .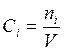

Подставляя в (5.8) r из (5.17) и учитывая, что согласно определению (2.4) , а значит,

, ;

, .                                      (5.18)

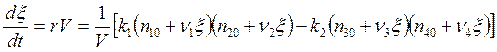.               (5.19)

Проводя далее интегрирование при условии : , :  получим

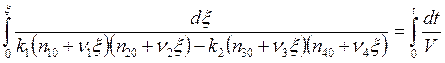,                       (5.20)

откуда можно получить

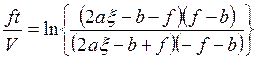,                                   (5.21)

где ; ; ; .

В соответствии с (2.8) степень превращения .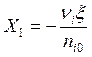

Селективность в данном случае  по любым реагентам, так как имеет место единственная реакция.

В случае простой реакции (5.16) (выполняется закон действующих масс , ). При этих значениях , , ,  соотношение (5.21) совпадает с соотношением, приведенным в табл. 5.1.

5.2.2 Две последовательные реакции 1-го порядка (dT/dt = 0)

j= 1: ,         и        j = 2: , .

Будем полагать, что закон действия масс может не выполняться, т.е.  - произвольные.

В соответствии с (2.6) , следовательно,

;         ;        .        (5.22)

Подставляя , и (5.22) в (5.8) и учитывая, что

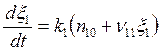;                                         (5.23)

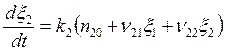;                              (5.24)

,      (или ,          ).                (5.25)

Интегрируя (5.23) и подставляя  в (5.24), получим

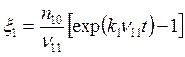;                                     (5.26)

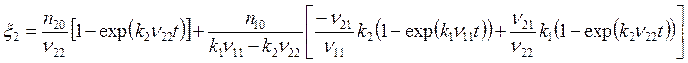. (5.27)

Степень превращения , так как в соответствии с (2.8)  (j = 1, 2).

Вычисление селективности и выхода. Пусть целевой продукт - А₂.

В соответствии с определением (2.15) мгновенная селективность

.                                                (5.28)

Отсюда, после подстановки dn₂ и dn₁, полученных из (5.22),

.

Или с учетом (5.23), (5.24)

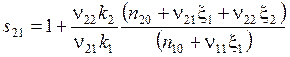,                                       (5.29)

где ξ₁ и ξ₂ - из уравнений (5.26), (5.27).

Интегральная селективность в соответствии с (2.10) и (2.18)

.                           (5.30)

Выход

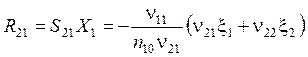.                                    (5.31)

Из (5.31) в случае n₂₀=0 (вещество A₂ в начальный момент в реакторе отсутствует) можно получить

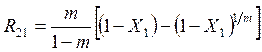,                                  (5.32)

где .

Из (5.32) видно, что выход R₂₁ в рассматриваемом случае является экстремальной функцией от степени превращения Х₁. Из условия  можно найти, что максимальный выход и соответствующее ему значение степени превращения определяются соотношениями

;       .                      (5.33)

С увеличением m (увеличение скорости превращения А₁)  возрастает.

Решение для некоторых других типов реакций (Т = const) представлены в таблице 5.1.

Таблица 5.1.

Схема реакции	Кинетическое соотношение	Порядок реакции	Уравнения баланса массы
			Дифференциальное	Интегральное
		0
		1
		1
		2 ()
		2		где
		1
		1