НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра "Автоматизации производственных процессов в машиностроении"
КУРСОВАЯ РАБОТА
"Анализ и синтез линейной системы автоматического управления"
ВЫПОЛНИЛА:
студентка гр. КП-32
Киселева И.Е.
ПРОВЕРИЛ:
Нос О.В.
Новосибирск 2006
Исходные данные для проектирования:
- номер варианта таблицы уравнений структурной схемы №8;
- номер варианта таблицы параметров объекта управления №6;
- допустимая скоростная ошибка регулирования Δyдоп(∞) = 0,001…0,005;
- максимально-допустимое время регулирования tp= 0,5... 1,5 с;
- максимально-допустимое перерегулирование σ% = (20...30)%.
Содержание пояснительное записки:
- определение ошибки регулирования по управляющему и возмущающему воздействиям в установившемся процессе;
- исследование устойчивости исходного объекта управления;
- определение требуемого коэффициента передачи последовательного корректирующего устройства;
- синтез линейной САУ на основании метода желаемых логарифмических частотных характеристик;
- проверка результатов синтеза методом цифрового моделирования.
Система обыкновенных дифференциальных уравнений, описывающая динамику исходной САУ:
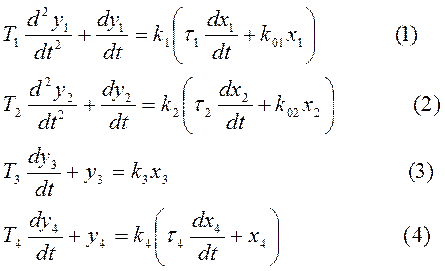
1. Анализ линейной САУ:
1.1. В соответствии с таблицей Т.1 составить структурную схему исходной нескорректированной САУ.
|
Уравнения связей |
||||
|
8 |
x3=(x - y) |
x4 = y3 – y2 |
x2 = y4 |
x1= y2 - z |
|
k1 |
τ1 |
T1 |
k01 |
k2 |
τ2 |
T2 |
k02 |
k3 |
T3 |
k4 |
τ4 |
T4 |
|
|
6 |
1.2 |
1 |
0.6 |
0 |
1.0 |
0.4 |
0 |
1.0 |
1.4 |
0.1 |
1 |
0.0 |
0.0 |
Примечание: х – задающее воздействие; z– возмущающее воздействие; хi– входная переменная i-ого звена; yi– выходная переменная i-ого звена; у = y1 – выходная (управляемая) переменная САУ.
Принципиальная схема:
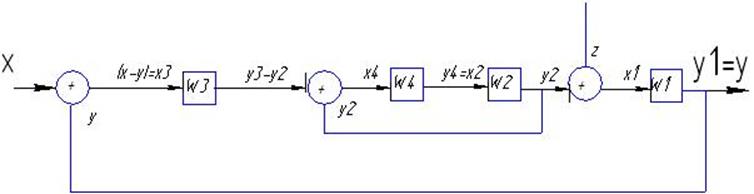
1.2. На основании дифференциальных уравнений (1) – (4) и таблицы Т.2 записать дифференциальные уравнения в операторной форме записи в общем виде и с учетом численных значений.
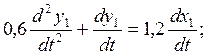 (5)
(5)
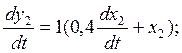 (6)
(6)
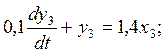 (7)
(7)
![]() (8)
(8)
В операторной форме:
![]()
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
1.3. Получить передаточные функции звеньев структурной схемы в стандартном виде.
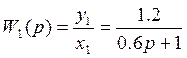 ;
;
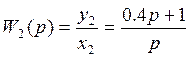 ;
;
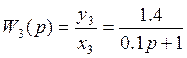 ;
;
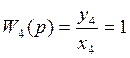 ;
;
Для наглядности впишем их в символы элементов на структурной схеме:
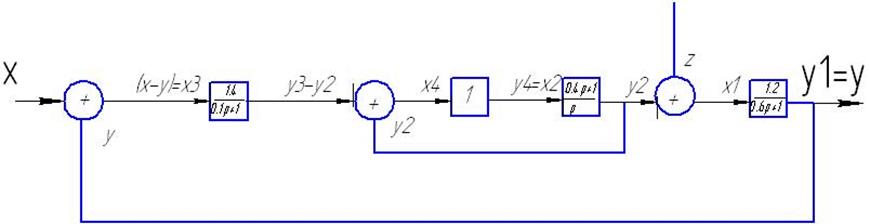
Преобразуем структурную схему к одноконтурной и определим передаточную функцию разомкнутой системы Wpaз(p), выделив в ней коэффициент передачи разомкнутой системы kраз.
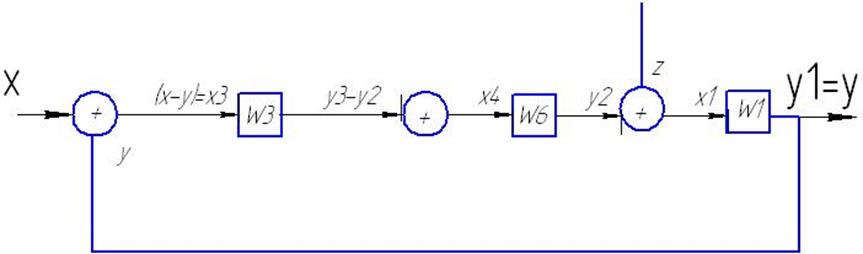
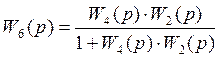 ;
;
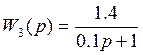 ;
; 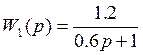
Передаточная функция разомкнутой системы:
![]() =
= ![]()
![]()
![]() =
= 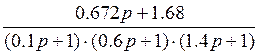
Коэффициент передачи разомкнутой системы:
![]()
1.4. Записать передаточные функции замкнутой САУ по задающему х и возмущающему z воздействиям и определить статические ошибки при нулевых начальных условиях в случае приложения единичного ступенчатого сигнала.
Передаточная функция замкнутой системы по управлению:
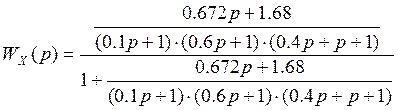 ;
;
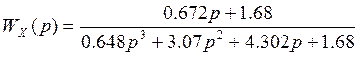 ;
;
Передаточная функция замкнутой системы по возмущению:
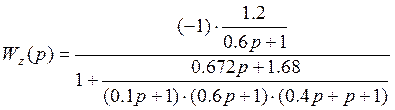 ;
;
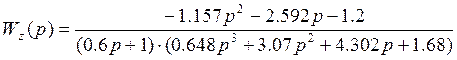 ;
;
Определение статических ошибок:
По управлению (при
нулевых начальных условиях p=0): ![]() =1
=1
По возмущению (при
нулевых начальных условиях p=0): ![]() = -0,714
= -0,714
1.5. При помощи алгебраического критерия устойчивости Гурвица проверить условие устойчивости нескорректированной САУ.
Запишем операторный полином:
![]() , где:
, где: ![]() ;
; ![]() ;
;
![]() ;
; ![]()
Для устойчивости линейной системы необходимо и достаточно, чтобы
![]() ;
; ![]() ;
;
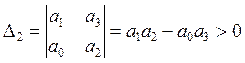 ;
;
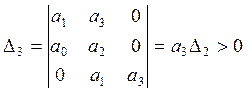 , т.е.
, т.е. ![]()
То есть
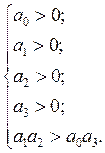
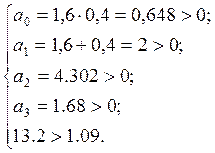
Достаточное условие устойчивости выполняется.
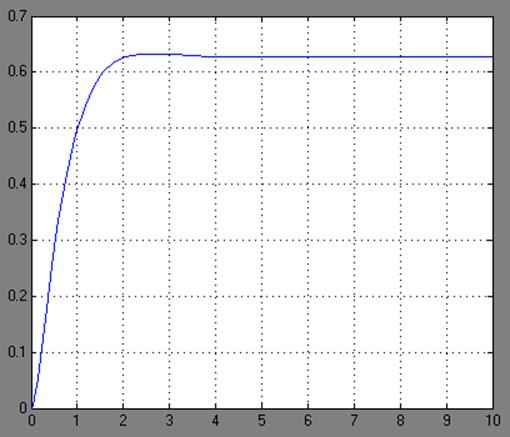
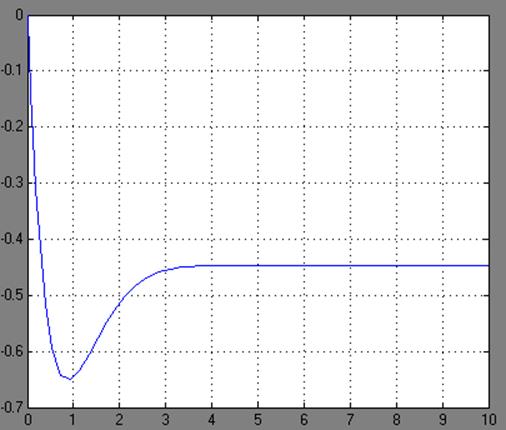
1.6. Методом цифрового моделирования определить прямой показатель качества переходных процессов и статическую точность регулирования (ошибку) нескорректированной САУ по двум внешним воздействиям х и z . Установившиеся значения выходной переменной у сравнить с результатами, полученными в п. 1.4.
Полная ошибка регулирования:
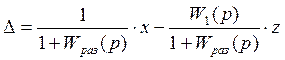
Передаточная функция ошибки по управлению:
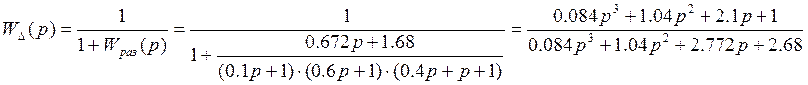
Передаточная функция ошибки по возмущению:
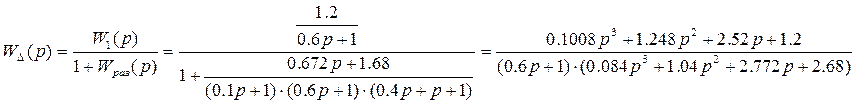
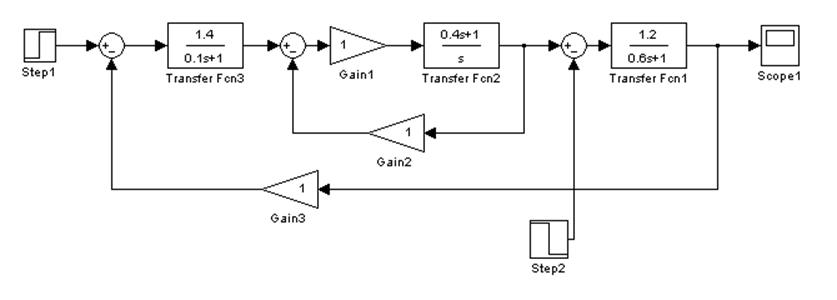
Схема исходной САУ:
Единичное ступенчатое воздействие по управлению:
Единичное ступенчатое воздействие по возмущению:
2. Синтез линейной САУ
2.1 Изобразить асимптотическую ЛАЧХ
нескорректированной системы ![]() c использованием логарифмического масштаба ω или lgω.
Продольную ось
c использованием логарифмического масштаба ω или lgω.
Продольную ось ![]() провести
через единичную частоту ω = 1.
провести
через единичную частоту ω = 1.
2.2 Построить желаемую ЛАЧХ астатической
скорректированной САУ ![]() , обеспечивающей заданные показатели качества переходных
процессов σ%, tр и требуемую скоростную ошибку
, обеспечивающей заданные показатели качества переходных
процессов σ%, tр и требуемую скоростную ошибку ![]() , которая
состоит из низкочастотной (НЧ), среднечастотной (СЧ) и высокочастотной (ВЧ)
областей.
, которая
состоит из низкочастотной (НЧ), среднечастотной (СЧ) и высокочастотной (ВЧ)
областей.
2.2.1 Наклон НЧ области желаемой ЛАЧХ
принять равной -20 дБ/дек. Требуемый разомкнутый коэффициент передачи ![]() скорректированной
системы определить как:
скорректированной
системы определить как:
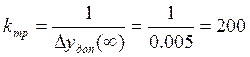
2.2.2 По номограммам, приведенным в [1,
стр. 230], задавшись значением перерегулирования σ%=30% и временем
регулирования tр = 0,5, определив максимальное значение вещественной
частотной характеристики ![]() =1,27 , находим частоту
среза
=1,27 , находим частоту
среза ![]() =1,34 и
необходимый запас устойчивости
=1,34 и
необходимый запас устойчивости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.