Моделирование синтезированной модифицированным модальным методом системы

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

Расчетно-графическая работа

по дисциплине

«Теория автоматического управления»

Факультет:	МТ
Группа:	КП-91
Студент:	Алексеев М.А.
Преподаватель:	Зима Е.А.

Новосибирск 2003г.

Вариант № 1 (схема - 1, строка таблицы - 1)

Исходные данные.

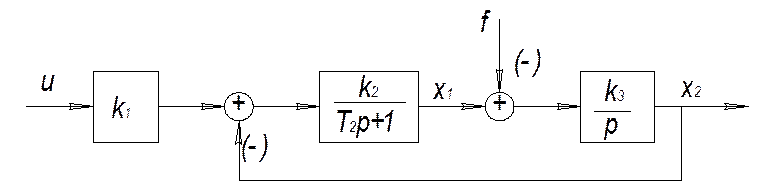
Рис.1. Структурная схема объекта управления.

Задание

1. Синтезировать алгоритм модального управления заданным объектом при полных измерениях и настройки системы на желаемое распределение корней характеристического полинома, соответствующее стандартной форме Баттерворта.

Среднегеометрический корень характеристического полинома САУ принять     равным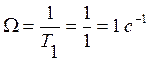   

2.  Синтезировать наблюдатель Люенбергера полного порядка с тем же распределением корней характеристического полинома и среднегеометрическим корнем. 

В качестве измеряемой координаты вектора состояния – координата

3.  Синтезировать наблюдатель Люенбергера пониженного порядка с быстродействием, заданным в пункте 2.

4.  Произвести синтез замкнутой системы при полных измерениях на основании модифицированного модального метода с распределением корней характеристического полинома и быстродействием, заданным в пункте 1.

1. Синтез алгоритма  модального управления.

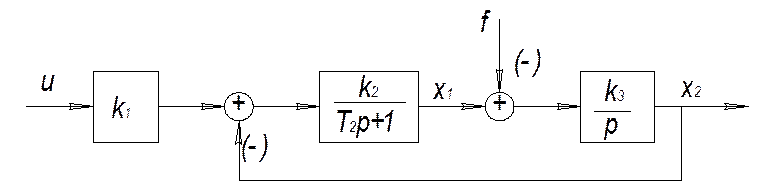
Рис.2. Структурная схема объекта управления.

График переходного процесса объекта управления по управляющему воздействию.

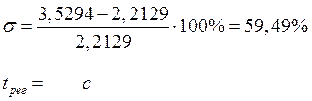
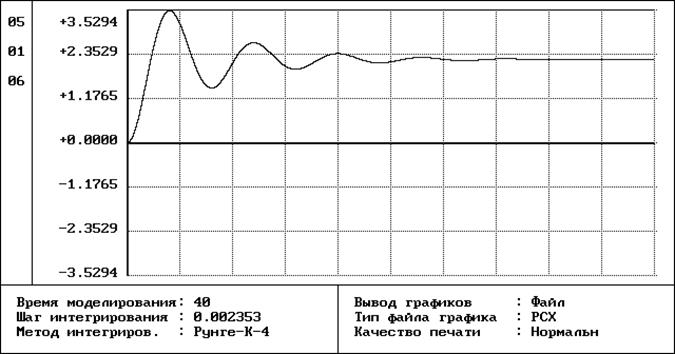
График переходного процесса объекта управления по возмущающему воздействию.

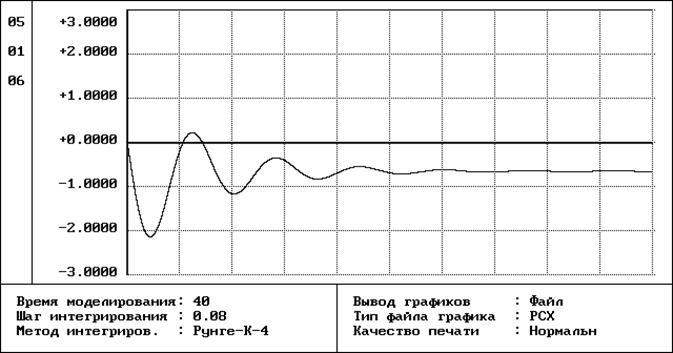
Показатели качества переходного процесса исходной системы: перерегулирование - s% = 59,49% , время регулирования t_р =      с.

Вывод: Полученные результаты нас не удовлетворяют. Чтобы добиться нужного качества переходного процесса необходимо синтезировать систему методом модального управления.

Математическое описание объекта управления, заданное структурной схемой, в виде дифференциальных уравнений в нормальной форме Коши: 

  ,

             , ,

 

,

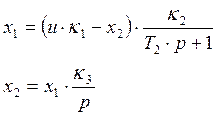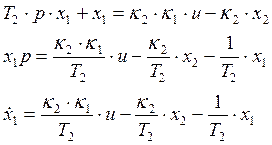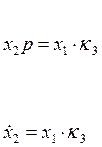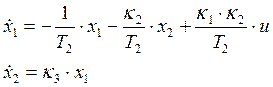Векторно-матричная модель заданного объекта:

, где       ,               ,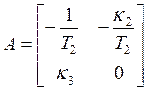  

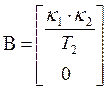– матрицы коэффициентов; dim A = n´n, dim B = n´1.

Проверка условия управляемости.

Для полной управляемости заданного объекта необходимо и достаточно, чтобы rang матрицы управляемости, составленный по правилу:   , был равен порядку системы rang y = n; dim y = n´(m´n).

,   ,

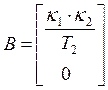
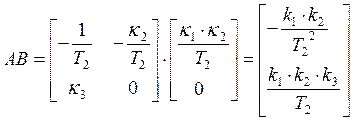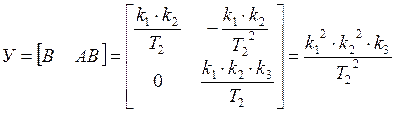
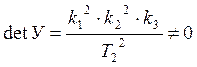
                   условие управляемости выполняется.

Характеристический полином замкнутой системы:

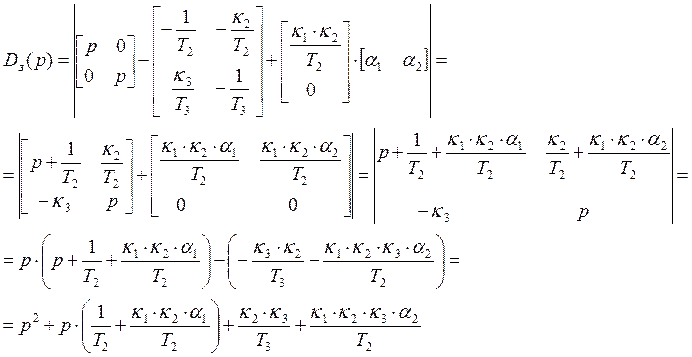
Синтез модального регулятора.

Закон управления:

, 

где  v – вектор новых управляющих или задающих воздействий, dim v = m;

        К – матрица коэффициентов обратных связей К = [a₁   a₂], dim K = m´n.

Для определения коэффициентов обратной связи характеристический полином замкнутой системы приравнивают к нормированному полиному вида:

N(p) = pⁿ + A_n-1Wp^n-1 + … +A₁W^n-1p + Wⁿ, где  А_i, i =  –  коэффициенты формы, определяющие форму переходного процесса;

 –  среднегеометрический корень характеристического уравнения; косвенно характеризует быстродействие

;      так как

                                          

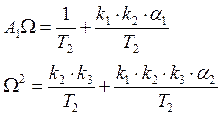
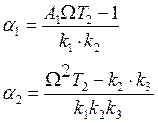
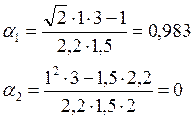
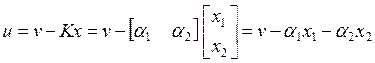
Структурная схема замкнутой системы.

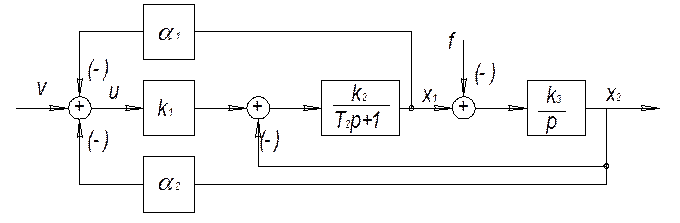
Рис.3. Структурная схема САУ с модальным управлением и полными измерениями.

Исследуем методом цифрового моделирования:

1) систему модального управления с измеряемыми координатами по управляющему воздействию.

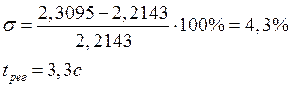
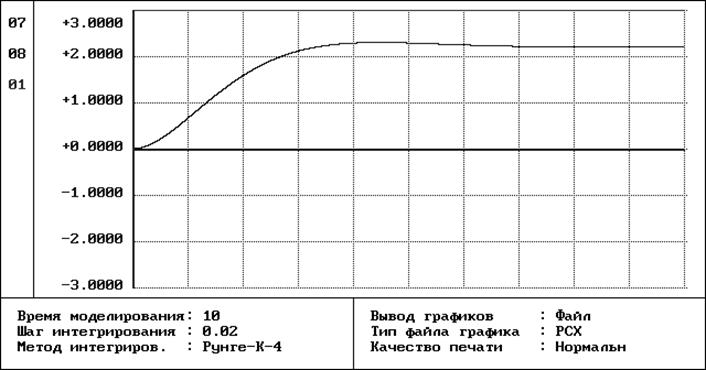
2) систему модального управления с измеряемыми координатами по возмущающему воздействию.

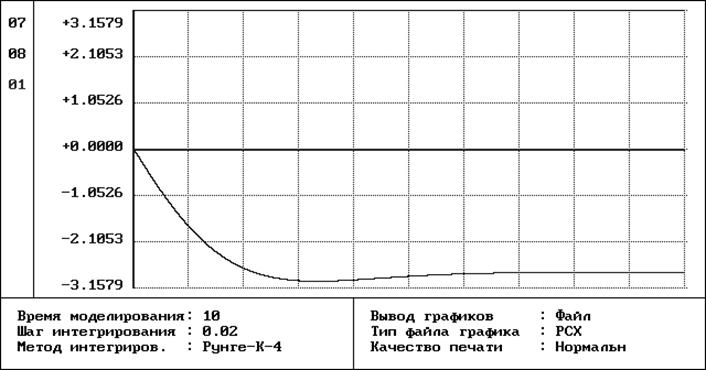
Вывод: В итоге, после дополнения структуры объекта обратными связями по координатам состояния с коэффициентами передачи  в синтезированной системе наблюдается нормированный переходной процесс, по форме соответствующей переходному процессу в системе при настройке на стандартную форму Баттерворта и имеющая показатели качества:

- перерегулирование  

- время регулирования .

Время регулирования переходного процесса уменьшилось, перерегулирование близко к желаемому. Быстродействие синтезируемой системы косвенно определяет