Исследование характеристик пульсаций в сверхзвуковом потоке в канале квадратного сечения, страница 5

2) Показатель n » 0,5 для сверхзвуковых скоростей.

3) Коэффициенты А и B являются константами.

Проведенные экспериментальные исследования показали, что имеется зависимость числа Нуссельта от степени нагрева нити Nu = Nu_e f, где Nu_e –для ненагретой нити. Поэтому зависимость (2.2) лучше использовать в виде

,                                    (2.3)

С учетом изложенного выше уравнение (2.1) для сверхзвуковых скоростей можно переписать в виде

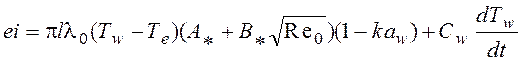.            (2.4)

Это уравнение будет использовано при получении выражений для коэффициентов чувствительности термоанемометрических датчиков, постоянных времени, при анализе их взаимосвязи.

2.1.2 Определение коэффициентов чувствительности датчиков

Возможны различные способы определения коэффициентов чувствительности: либо экспериментально из непосредственной тарировки каждого датчика, либо аналитически с использованием теоретических и полуэмпирических соотношений.

Как следует из формулы (2.4), кроме силы тока, определяемой конструктивными особенностями датчика и перегревом, напряжение на датчике термоанемометра зависит от температуры торможения потока Т₀, массового расхода газа m и перегрева датчика а_w :

е = е (m, Т₀, a_w ).                                              (2.5)

Теплопроводность газа l  зависит от температуры торможения:

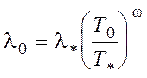                                                (2.6)

Разность температур (T_w - T_e) легко выражается через перегрев а_w  и температуру торможения Т₀:

(T_w - T_e ) = а_w [1 + a_*(hТ₀ - T_*) ] a_*^-1.                          (2.7)

Здесь использована линейная зависимость электрического сопротивления R от температуры Т:

R = R_* [1 + a_*(T - T_*)],                                           (2.8) где a_*– температурный коэффициент сопротивления датчика,

Опуская преобразования, аналогичные приведенным в разделе 2.3.1 запишем

,                   ,                ,

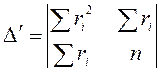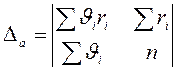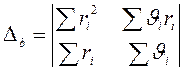    ,                                .                                                 (2.79)

Используя вычисленные значения определителей (2.79)

,          ,         ,          ,

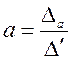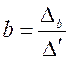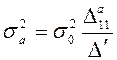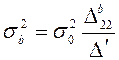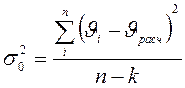.                                       (2.80)

Рассчитанные по этим формулам погрешности приведены в таблице 2.1.

Таблица 2.1 – Погрешности определения характеристик пульсаций параметров потока

3 АНАЛИЗ РЕЗУЛЬТАТОВ

Ранее были получены значения выходного напряжения от различной степени нагрева датчика термоанемометра. Эти сигналы были обработаны и построены диаграммы пульсаций. Диаграммы пульсаций в рабочей части при установленных решетках показаны на рисунке 3.1.

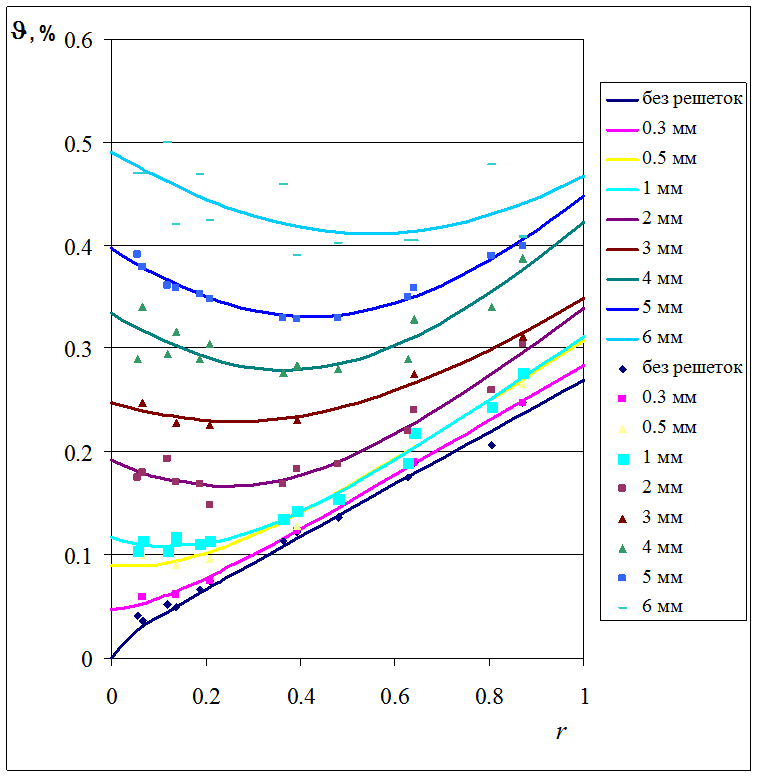
Рисунок 3.1 —  Диаграммы пульсаций в рабочей части при установленных решетках

Точки построены по экспериментальным данным. Кривые получены при помощи метода наименьших квадратов с использованием уравнения гиперболы  (2.71). Нижняя прямая получена при отсутствии решеток и соответствует акустическим возмущениям, генерируемым пограничным слоем на стенках рабочей части.

В первых столбцах таблицы 3.1 приведены значения <m>_S , <T_o>_S и (R_mT0)_S, соответствующие суммарным пульсациям, которые генерируются решетками и пограничным слоем на стенках сопла и рабочей части.

Таблица 3.1 — Таблица значений