








7 Однофазный трубчатый реактор. 73
7.1 Реактор идеального вытеснения. 75
7.1.1 Решения для простых случаев. 76
7.2 Влияние обратного перемешивания. 78
7.3 Существующие технологии. 80
7 Однофазный трубчатый реактор
Это также проточный реактор (открытая термодинамическая система), однако в отличие, от реактора идеального перемешивания трубчатый реактор, как правило, характеризуется наличием градиентов концентрации и температуры (рис. 7.1).

Трубчатый реактор может быть выполнен в виде единичной трубы, обменивающейся теплом с внешней средой через стенку (рис. 7.1, ж), в виде пучка труб, охлаждаемых (нагреваемых) теплоносителем, трубы большого диаметра с внутренними теплообменниками и т.д.
Возможные профили скорости (u), коэффициентов дисперсии (D), концентрации (C) и температуры (т) показаны на рис. 7.1, а - д: (а) - поток с изменяющимися радиальным и осевым коэффициентами дисперсии (КД); (б) - осевой и радиальный КД постоянны; (в) - плоский профиль скорости (турбулентный поток); (г) - учитывается только осевая дисперсия, перемешивание в радиальном направлении - идеальное; (д) - идеальное радиальное перемешивание при отсутствии осевой дисперсии (идеальное вытеснение). На рис. 7.1, ж приведен материальный баланс для элементарного объема трубчатого реактора.
Режимы (г), (д) могут описываться на основе одномерных моделей. Режим (д) в котором осевая дисперсия отсутствует, называется режимом идеального вытеснения или поршневым режимом.
Рассмотрим одномерную модель трубчатого реактора.
Пусть, как и прежде, реакционная система характеризуется стехиометрическим уравнением (5.1)
![]() ,
, ![]()
(![]() ,
, ![]() ,
, ![]() - для
инерта).
- для
инерта).
В одномерном случае ограниченного перемешивания уравнения баланса массы и энергии имеют вид (4.8) и (4.9):
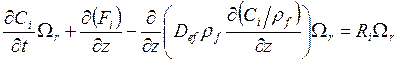 ;
;
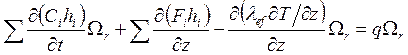 ,
,
(i, … S)
или в терминах концентрации и температуры (4.10), (4.11)
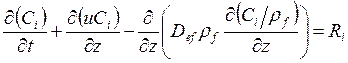 ;
;
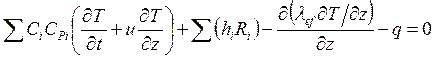 ,
,
![]() .
.
7.1 Реактор идеального вытеснения
Так как в случае идеального вытеснения Def = 0 и lef = 0, то в условиях стационарного режима (4.8) и (4.9) можно записать в виде
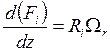 ,
, ![]() ; (7.1)
; (7.1)
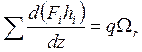 ,
, ![]() (7.2)
(7.2)
или в терминах концентрации и теплоемкости из (4.9), (4.10)
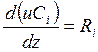 ,
, ![]() ; (7.3)
; (7.3)
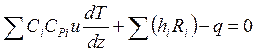 ,
, ![]() . (7.4)
. (7.4)
Уравнения (7.1) и (7.2) можно преобразовать и записать в терминах химической переменной, если учесть, что в соответствии с (2.7) и (5.1)
![]() , а
, а ![]() ;
;
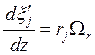 ,
, ![]() . (7.5)
. (7.5)
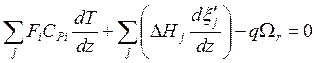 ,
, ![]() . (7.6)
. (7.6)
Чтобы получить уравнение (7.6), необходимо было учесть
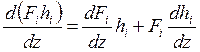 ;
;
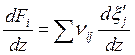 ;
; 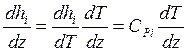 ;
;
![]() (см.
вывод (6.6)).
(см.
вывод (6.6)).
R уравнений (7.5) и уравнение (7.6) могут быть проинтегрированы совместно как единая система уравнений, если заданы граничные условия, например,
z = 0: Fi = Fi0, (или ξj = 0 (j = 1, ...,R)), т = т0. (7.7)
Для конкретного случая необходимо задать конкретные
стехиометрические соотношения и вид зависимости для q. Например, если
теплообмен осуществляется через стенку реактора (![]() ,
, 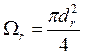 ,
, ![]() ),
),
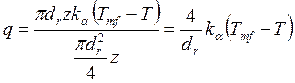 . (7.8)
. (7.8)
Здесь kα - коэффициент теплопередачи между теплоносителем и реакционной средой; dr - диаметр реактора; Tmf - температура теплоносителя.
В общем случае величины kα, тmf, Т могут быть функцией z.
В этом случае систему уравнений (7.5), (7.6), (7.8) необходимо дополнить еще двумя уравнениями, определяющими зависимости для kα и тmf. В частности, для тmf, можно записать
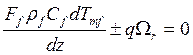 , (7.9)
, (7.9)
где Ff, ρf, Cf - расход, плотность и теплоемкость теплоносителя.
При этом граничные условия:
тmf = тmf0 для z = 0 (в случае прямотока);
тmf = тmfz для z = Z(в случае противотока).
7.1.1 Решения для простых случаев
Наиболее простыми являются:
1) изотермический реактор (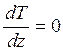 );
);
2) адиабатический реактор (q = 0).
Рассмотрим первый случай, при наличии одной реакции ![]() , протекающей в трубчатом реакторе.
, протекающей в трубчатом реакторе.
Уравнение (7.5) в этом случае имеет вид
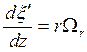 . (7.10)
. (7.10)
Пусть для определенности
имеет место реакция первого порядка (т.е. ![]() ,
, ![]() где
где ![]() ). В
этом случае (7.10) имеет вид
). В
этом случае (7.10) имеет вид
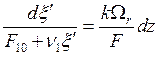 . (7.11)
. (7.11)
Откуда для случая F = const легко получить
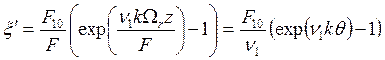 , (7.12)
, (7.12)
где ![]() - объем реактора, необходимый для достижения
показателя превращения
- объем реактора, необходимый для достижения
показателя превращения ![]() ;
; ![]() - время
пребывания реакционной среды в реакторе в момент прохождения сечения z.
- время
пребывания реакционной среды в реакторе в момент прохождения сечения z.
Таким образом, в соответствии с (7.12) изменение ![]() (или Fi, или Ci) по длине трубчатого
реактора идеального вытеснения (или на выходе из реактора) определяется только
временем пребывания реакционной среды в реакторе в момент прохождения
соответствующего сечения z. Для простой реакции первого порядка А1
→ А2 (
(или Fi, или Ci) по длине трубчатого
реактора идеального вытеснения (или на выходе из реактора) определяется только
временем пребывания реакционной среды в реакторе в момент прохождения
соответствующего сечения z. Для простой реакции первого порядка А1
→ А2 (![]() ) (7.12) переходит в
) (7.12) переходит в
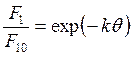 . (7.13)
. (7.13)
Это уравнение совершенно аналогично соответствующему для периодического реактора (см. табл. 5.1)
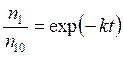 .
.
Совершенно одинаковый вид имеют и выражения для конверсии вещества Аi, соответствующие периодическому реактору и реактору идеального вытеснения:
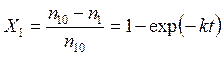 -
периодический реактор;
-
периодический реактор;
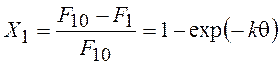 -
реактор идеального вытеснения.
-
реактор идеального вытеснения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.