Однофазный трубчатый реактор. Реактор идеального вытеснения. Влияние обратного перемешивания, страница 2

Отмеченная аналогия имеет общий характер. Все соотношения, представленные в табл. 5.1, справедливы и для реактора идеального вытеснения, если только в них время реакции t заменить на время пребывания θ, a n_i на F_i. Соответствие между реакторами двух типов вполне понятно. Действительно, реакционная смесь в реакторе идеального вытеснения движется без перемешивания в осевом направлении. При этих условиях любой элементарный объем реакционной среды может рассматриваться как периодический микрореактор, перемещающийся в пространстве, который начинает работать при t = 0 и заканчивает при t = θ. Если реактор адиабатический, то и температурные зависимости от времени идентичны, т. е. Т(θ) = Т(t). В случае неизотермического реактора условием идентичности соотношений, описывающих периодический реактор и реактор идеального вытеснения, является равенство Т(θ) = Т(t).

7.2 Влияние обратного перемешивания

Рассмотренные модели идеальных реакторов перемешивания и вытеснения отражают предельные ситуации, которые могут иметь место в реальном реакторе. В реакторе идеального перемешивания порция меченого вещества, введенная в некоторой точке, мгновенно распределяется по всему объему реактора. В реакторе идеального вытеснения перемешивание отсутствует, поэтому введенная порция меченого вещества движется вместе с потоком не размываясь. Очевидно, что и в первом и во втором случаях проблема перемешивания автоматически исключается из рассмотрения при описании реактора. Для практики представляет интерес также промежуточный случай, когда перемещение газа или жидкости в реакторе сопровождается ограниченным перемешиванием. В этом случае порция меченого вещества, поданная в некоторую точку, с течением времени будет размываться и интенсивность размыва (скорость изменения концентрации) будет зависеть от интенсивности перемешивания вещества в реакторе. Механизмы перемешивания могут быть различными: за счет молекулярной и турбулентной диффузии, дисперсии скорости среды, наличием застойных зон и т. д.

Во многих случаях оказывается достаточным интенсивность перемешивания характеризовать эффективным коэффициентом диффузии (D_ef), а интенсивность теплопереноса за счет перемешивания - эффективным коэффициентом теплопроводности (l_ef) без рассмотрения конкретных механизмов перемешивания, как это и было сделано при выводе уравнений (4.10) и (4.11).

В приближении уравнений (4.10) и (4.11) математическая модель реактора называется диффузионной, так как используемые при этом уравнения формально полностью совпадают с уравнениями конвективной диффузии и теплопроводности.

Если свойства среды и скорость не зависят от z, то обозначив  и учтя, что , , (4.10) и (4.11) для случая q = 0 можно переписать в виде

;                                (7.14)

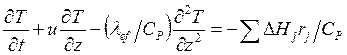,                            (7.15)

или, приводя к безразмерному виду (предварительно домножив (7.14) на , а (7.15) на ), эти уравнения можно записать следующим образом:

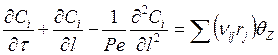;                               (7.16)

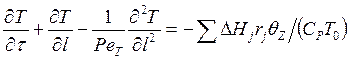,          ,       (7.17)

где ,  - диффузионный и тепловой критерии Пекле; ∆Н - теплота реакции; l = z/Z; t = t/θ_Z; Z - высота реактора; Т = T/T₀, T₀ - характерная температура, например температура потока на входе или температура в теплообменнике.

Граничные условия, выражающие неразрывность потоков вещества и тепла слева и справа входного и выходного сечений реактора, записываются в форме Данквертса

l = 0: ;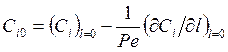

;

l = 1: , .                                      (7.18)

Рассмотрим простую реакцию первого порядка, протекающую в стационарных изотермических условиях (А₁ → А₂, R₁ = - kC₁). В этом случае необходимо единственное уравнение (7.16), которое принимает вид

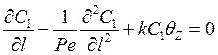.                                (7.19)

Это уравнение может быть проинтегрировано с учетом соответствующих граничных условий (7.18)

;

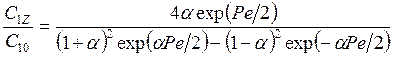.                                         (7.20)

Таким образом, при наличии ограниченного обратного перемешивания концентрация реагентов на выходе из реактора является функцией двух параметров kθ_Z и Ре.

В случае идеального вытеснения имеет место зависимость (7.13), которая в терминах концентрации имеет более простой вид

.                                            (7.21)

В случае слабого перемешивания (, т.е. ) уравнения (7.20) и (7.21) дают одинаковый результат.

7.3 Существующие технологии

Трубчатые реакторы применяются, как правило, для осуществления процессов при повышенных давлениях и повышенных температурах. В зависимости от уровня температур применяются два типа трубчатых реакторов:

1) с жидким теплоносителем (< 500°С, поддержание необходимой температуры (охлаждение или нагрев реактора) осуществляется за счет циркуляции воды, пара, высокотемпературных органических жидкостей или растворов, циркулирующих в межтрубном пространстве или «тепловой рубашке» реактора);

2) с нагревом реакционных труб продуктами сгорания за счет размещения реакционных труб в конвективной или радиационной зонах печи (> 500°с, трубы, как правило, прямые, длина 6-12 м).

Длина трубчатого реактора, диаметр, скорость реакционной среды, время контакта зависят от особенностей процесса (скоростей целевой и побочных реакций, теплового эффекта и др.) и находятся, как правило, в пределах Z > 10 м, d_r = 30÷100 мм, u = 8÷10 м/с.

Типичными процессами, осуществляемыми в трубчатых реакторах являются полимеризация этилена (P = 2000-3000 атм, т = 200-300°С, общая длина реактора – Z = 200-800 м, производительность 6-10 т/ч полиэтилена низкой плотности), паровой крекинг нефтяных фракций (T > 800°с) с получением олефинов (этилена, полипропилена), конверсия углеводородов в синтез-газ, производство винилхлорида из дихлорида этилена и др.