Циклические коды и их свойства

Циклическим кодом называется линейный блочный код (n,k), который характеризуется свойством цикличности, то есть сдвиг влево на один шаг любого разрешенного кодового слова дает другое разрешенное кодовое слово, принадлежащее этому же коду; множество кодовых слов циклического кода представляется совокупностью многочленов степени (n-1) и менее, делящихся на некоторый многочлен g(x) степени r = n-k, который является сомножителем двучлена xⁿ+1. Многочлен g(x) называется порождающим (или производящим).

Циклические коды образуют циклическую группу, в которой кодовые слова образуются путем умножения некоторого кодового слова на x ^j

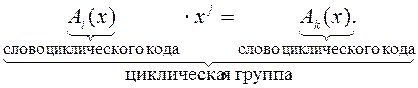
Кодирование циклического кода осуществляется путем деления информационной последовательности на производящий многочлен. Поэтому для формирования циклического кода достаточно знать производящий многочлен g(x), который определяется как наименьшее общее кратное (НОК) минимальных функций m_i(x) ,(см. глава 2)

g(x) =НОК{m₁(x)× m₂(x)×…× m_r(x)}.                               (3.1)

Одна из основных задач, стоящих перед разработчиками устройств защиты от ошибок при передаче дискретных сообщений по каналам связи, является выбор g(x) для построения циклического кода, обеспечивающего требуемое минимальное расстояние d для гарантийного обнаружения и исправления  t-кратных ошибок. Существуют специальные таблицы по выбору g(x) в зависимости от предъявляемых требований к корректирующим свойствам кода [2].

Однако каждая разновидность циклических кодов имеет свои особенности формирования g(x). Поэтому при изучении конкретных циклических кодов будут рассматриваться соответствующие способы построения g(x).

Длина кодового слова определяется как

n=2^m-1,                                                                 (3.2)

где m – расширение поля GF(2^m).

Число проверочных символов

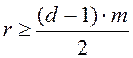,                                                                (3.3)

в свою очередь степень производящего многочлена равна .

Кодовое расстояние .

Производящая матрица циклического кода образуется путем умножения производящего многочлена  степени () последовательно на .

Проверочная матрица циклического кода определяется следующим образом

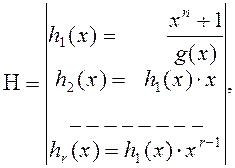                                                (3.4)

где  – строки проверочной матрицы.

Проверочная матрица позволяет построить проверочные соотношения и вычислить синдром ошибки в виде многочлена степени  (n-k-1)

                     (3.5)

где B(x) - многочлен принятого кодового слова степени (n-1), е(x) - многочлен ошибок в канале степени (n-1).

Для циклических кодов операция вычисление синдрома ошибки может быть записана в виде

Помимо основных циклических кодов существует класс укороченных (усеченных) циклических кодов, которые образуются путем уменьшения числа информационных символов. Они обладают такими же свойствами, что и основные коды: (n, k) – основной код, следовательно (n-1, k-1)…(n=r+1, k=1) – укороченные коды.

Если код предназначен для исправления и обнаружения независимых ошибок, то необходимо обеспечить соответствующее кодовое расстояние между кодовыми словами циклического кода. Лучшими кодами, обеспечивающими эффективную борьбу с независимыми ошибками, являются циклические коды Боуза-Чоудхури-Хоквингема (БЧХ). Эти коды являются обобщением кодов Хэмминга. Кодирование кодов БЧХ можно осуществлять с помощью регистра сдвига с обратными