










размещения АТС будет вершина а5, что при построении абонентской сети обеспечит минимальный расход кабеля на линейные сооружения.
Этап 4. На данном этапе в графе G выделяются кратчайшие пути от медианной вершины аx ко всем остальным вершинам. Именно эти пути соответствуют оптимальным трассам прокладки абонентского кабеля для подключения распределительных шкафов к районной АТС.
В теории графов указанная задача называется задачей построения дерева кратчайших путей для заданной вершины (в нашем случае это вершина аx, где планируется установка АТС). Будем использовать алгоритм Дейкстры, который основан на следующем простом факте: если известен кратчайший путь из вершины аs в вершину аj и вершина аk принадлежит этому пути, то кратчайший путь из аs в аk является частью указанного пути, который заканчивается в вершине аj. Имея в виду приведенное соображение, формальное описание алгоритма Дейкстры включает в себя следующие действия:
A) Помечается исходная (корневая) вершина аx и ей приписывается вес hx=0. Остальные вершины первоначально не помечены и их веса hi=¥ (i¹x). Для хранения номера последней из помеченных вершин предусматривается переменная k и на данном шаге k=x.
Б) Для каждой непомеченной вершины аi делается попытка уменьшить ее вес: hi=min{hi, hk+lki), где lki – вес ребра bki. Если после этих операций окажется, что hi=¥ у всех непомеченных вершин аi, то к ним отсутствуют пути из аk и работа алгоритма заканчивается.
B) Пусть из всех hi, относящихся к непомеченным вершинам, наименьшим является значение hr. В этом случае необходимо: пометить вершину аr и то ребро, ведущее к аr, вес которого определяет значение hr; значение r присвоить переменной k, т.е. теперь k=r. При наличии нескольких непомеченных вершин с одинаковым весом, величина которого является минимальной, произвольно выбирается одна из них и только для нее выполняются указанные операции.
Г) Если осталась хотя бы одна непомеченная вершина, то переходим к пункту Б, иначе процедура завершается и ее результатом является дерево кратчайших путей, которое образуется помеченными ребрами.
Построим дерево кратчайших путей для вершины а4 графа, показанного на рисунке 2. Последовательность действий будет состоять из следующих операций:
1) Весам вершин приписываем начальные значения h5=0 и h1=h2=h3=h4=h6=h7=h8=¥. Помечаем вершину а5 и ее номер присваиваем переменной k, т.е. k=5.
2) Для каждой непомеченной вершины пытаемся уменьшить вес:
h1=min(h1, h5+l51)=min(¥,0+¥)= ¥
h2=min(h2, h5+l52)=min(¥,0+2)=2
h3=min(h3, h5+l53)=min(¥,0+¥)=¥
h4=min(h4, h5+l54)=min(¥,0+3)=3
h5=min(h5, h5+l56)=min(¥,0+¥)= ¥
h7=min(h7, h5+l57)=min(¥,0+1)=1
h8=min(h8, h5+l58)=min(¥,0+¥)=¥
Из полученных величин h7 является минимальной, поэтому помечаем вершину а7 и ребро b57, вес которого определяет значение h7. Полагаем k=1.
3) h1=min(h1, h7+l71)=min(¥,1+¥)=¥
h2=min(h2, h7+l72)=min(2,1+¥)=2
h3=min(h3, h7+l73)=min(¥,1+¥)=¥
h4=min(h4, h7+l74)=min(3,1+¥)=3
h5=min(h5, h7+l76)=min(¥,1+4)=5
h8=min(h8, h7+l78)=min(5,1+3)=4
Помечаем вершину а2 и ребро b72, определяющее величину h2, (см. предыдущий шаг). Полагаем k=2.
4) h1=min(h1, h2+l21)=min(¥,2+3)=5
h2=min(h3, h2+l23)=min(¥,2+2)=4
h3=min(h4, h2+l24)=min(3,2+¥)=3
h5=min(h6, h2+l26)=min(5,2+)¥=5
h8=min(h8, h4+l28)=min(,¥2+4)=6
Помечаем, вершину а3 ребро b24 определяющее величину h3(см. шаг 2). После этого k=3
5) h1=min(h1 h3+l41)=min(5,3+2)=5
h2=min(h3, h3+l43)=min(4,3+5)=4
h6=min(h6, h3+l46)=min(5,3+5)=5
h8=min(h8, h3+l48)=min(6,3+4)=6
Помечаем вершину a2 и ребро b43 вес которого определяет величину h2 (см. шаг 3). Полагаем k=4
6) h3=min(h3, h1 +l13)=min(4,5+5)=4
h6=min(h6, h1+l16)=min(5,5+5)= 5
h8=min(h8,h1+l18)=min(6,5+¥)=6
Помечаем вершину a3 и ребро b13, определяющее величину h3 (см. шаг 3). Теперь k=4
7) h6=min(h6, h3+l36)=min(5,4+5)=5
h3=min(h8, h3+l38)=min(6,4+6)=6
Помечаем вершину a6, а также ребро b36, которое определяет величину h6 (см. шаг 4). В результате k=5
8) h8=min(h8, h6+l68)=min(6,5+6)=6
Помечаем последнюю вершину а и ребро b53, вес которого на шаге 5 определял величину h3. На этом работа алгоритма заканчивается, а полученное дерево кратчайших путей показано на рисунке 3.
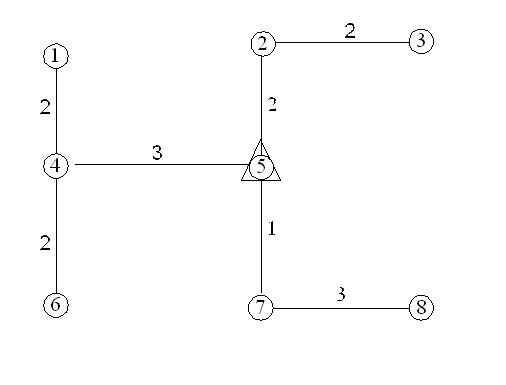
Рисунок 3
Этап 5. Для проводного радиовещания или кабельного телевидения задача построения на рассматриваемой территории города ретрансляционной сети с минимальной стоимостью сводится к выделению из графа G связного подграфа, включающего в себя все вершины из множества А и имеющего наименьшую суммарную длину ребер. Такой подграф всегда является деревом и называется также кратчайшим остовом графа G.
Для получения оптимальной структуры связывающей сети с минимальной общей длиной имеется алгоритм Прима-Краскала, который
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.