Лишь после вычислений параметров участков можно переходить к определению токов. Ток в неразветвленной части цепи и коэффициент мощности находятся по формулам:
I = ![]() ;
; ![]()
Напряжение на зажимах разветвления:
![]() = I
= I![]()
Ток в левой ветви:
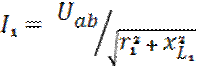
Ток в правой ветви:
![]() =
= ![]()
3. При включении в цепь индуктивности L часто говорят об индуктивном сопротивлении, индуктивном падении напряжения или индуктивной составляющей напряжения. Однако в действительности в этих понятиях есть условность. При включении в цепь катушки, обладающей активным сопротивлением r и индуктивностью L, на переменное синусоидальное напряжение и уравнение по второму закону Кирхгофа записывается так:
u= ir+(—eL). Это объясняется следующим: часть напряжения от и падает в сопротивлении r (т. е. ir), а остальная часть — на компенсацию возникающей L ЭДС самоиндукции (т. е. — еL). Численно же величина возникающей ЭДС.
4. EL= -ωLI. Так как ωL выражается в омах, то xl=ωLназывают реактивным индуктивным сопротивлением, а произведение xlIназывают индуктивным падением напряжения (по аналогии с произведением rI).
5.Следует обратить внимание на то, что понятия активной и реактивной проводимостей имеют условно-расчетный характер. Например, для параллельно включенной катушки с сопротивлением r и индуктивностью Lактивная проводимость, определяемая по формуле:
g = ![]() ,
,
включает в себя не только активное сопротивление r, но и индуктивное xL. Аналогично в формулу индуктивной проводимости
![]() =
= ![]()
входит не только индуктивное сопротивление xL , но и активное r.
5. Изучая явления резонанса, необходимо усвоить следующее. При резонансе напряжение и ток на зажимах цепи всегда совпадают по фазе. Настройка же цепи на резонанс зависит от схемы соединений индуктивности и емкости. Для последовательной цепи условием резонанса является равенство индуктивного и емкостного сопротивлений: xL=xC. Для цепи, содержащей параллельный контур, в одной из ветвей которого находится индуктивность, а в другой — емкость, условием резонанса является равенство реактивных проводимостей ветвей: bL = bc.
6. При выполнении расчетов по методу комплексных чисел следует иметь в виду, что вещественная и мнимая части комплексного сопротивления, комплексной проводимости и комплексной мощности всегда представляют собой соответственно активную и реактивную составляющие этих величин; что же касается комплексного напряжения и комплексного тока, то такое положение имеет место лишь в частных случаях. Вещественная и мнимая части комплексного напряжения и комплексного тока определяются начальными фазами вели- чин, иначе говоря, зависят от расположения соответствующих векторов относительно осей комплексной плоскости, тогда как их активная и реактивная составляющие определяются углом сдвига по фазе φ между этими двумя векторами.
Если ψi=0 (вектор тока
расположен на комплексной плоскости вдоль вещественной оси в положительном
направлении), то ![]() =Ieiф=I. В этом случае:
вещественная часть комплексного тока равна I, мнимая - 0;
вещественная часть комплексного напряжения равна Ucos ψu, мнимая - Usinψu. Но так как в
данном случае ф=ψu-ψi=ψu , то
=Ieiф=I. В этом случае:
вещественная часть комплексного тока равна I, мнимая - 0;
вещественная часть комплексного напряжения равна Ucos ψu, мнимая - Usinψu. Но так как в
данном случае ф=ψu-ψi=ψu , то
![]() =
= ![]() =
= ![]() ;
; ![]() =
= ![]() =
= ![]() , и,
следовательно, разложение комплексного напряжения (но не тока) на вещественную
и мнимую части совпадает с разложением напряжения на активную и реактивную
составляющие.
, и,
следовательно, разложение комплексного напряжения (но не тока) на вещественную
и мнимую части совпадает с разложением напряжения на активную и реактивную
составляющие.
Если же ψu=0
(вектор
напряжения расположен на комплексной плоскости вдоль вещественной оси в
положительном направлении),то ![]() =
= ![]() .
.
В этом случае, вещественная часть комплексного напряжения равна
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.