Линейные цепи постоянного тока. Определение токов во всех ветвях методом контурных токов

Задание 1.

Линейные цепи постоянного тока.

Задача. Для электрической схемы (рис 1.9) выполнить следующее:

1.  Составить на основании законов Кирхгофа систему уравнений для расчета тока во всех ветвях схемы.

2.  Определить токи во всех ветвях методом контурных токов.

3.  Определить токи во всех ветвях схемы методом узловых потенциалов.

4.  Результаты расчета токов, проведенного двумя методами свести в таблицу и сравнить между собой.

5.  Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

6.  Определить ток  I₁  в заданной по условию схеме с источником тока методом эквивалентного генератора.

7.  Начертить потенциальную диаграмму для любого замкнутого контура, включающего в себя обе  ЭДС.

 

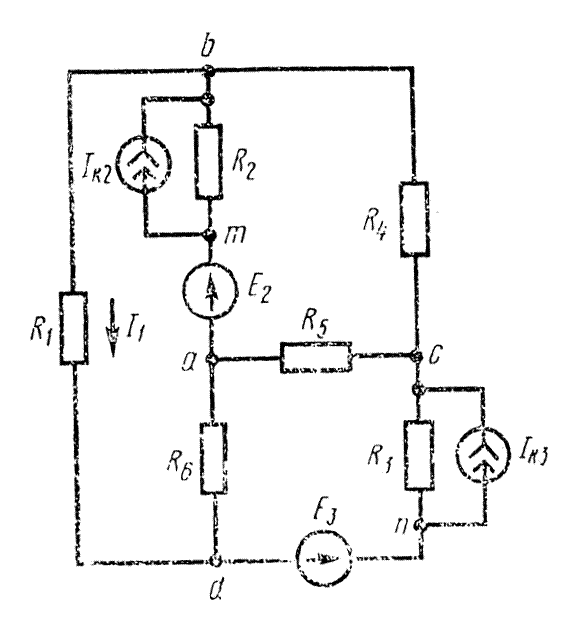Исходные Данные.

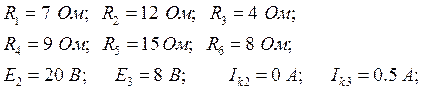
1.  Составить на основании законов Кирхгофа систему уравнений для расчета тока во всех ветвях схемы.

Проведем эквивалентное преобразование источника тока в источник ЭДС.

Исключим из схемы E_k2 (т.к  E_k2=0);

 

 

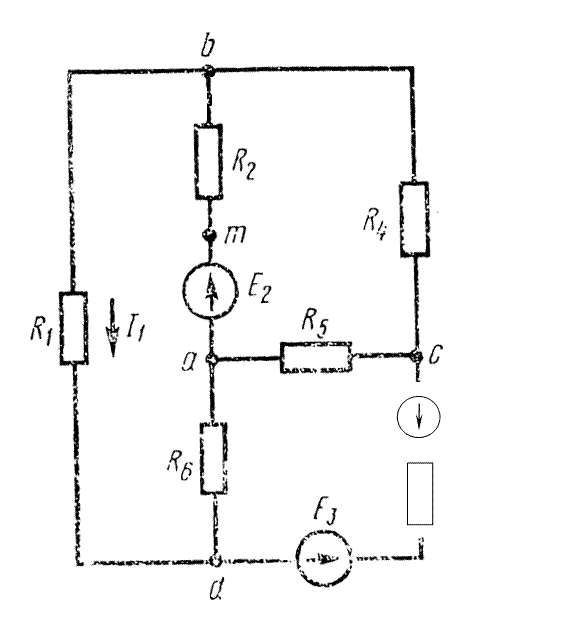
Число ветвей с активными и пассивными элементами  (ac, ad, ab, dc, cb, db) В = 6;

Узлов (a, b, c, d)  у = 4;

Первый закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет составить (у–1) уравнений.   у – 1=3;

Недостающие уравнения в количестве  в – (у – 1) = 6 – (4 – 1) = 3 составляют исходя из второго закона Кирхгофа. Уравнения записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.

Общее количество уравнений в – (у – 1)+ (у–1) = 6;

По первому закону Кирхгофа

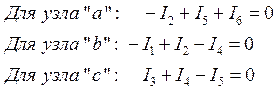
По первому закону Кирхгофа

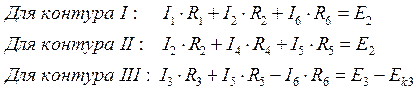
2. Рассчитаем токи во всех ветвях методом контурных токов (МКТ).

 

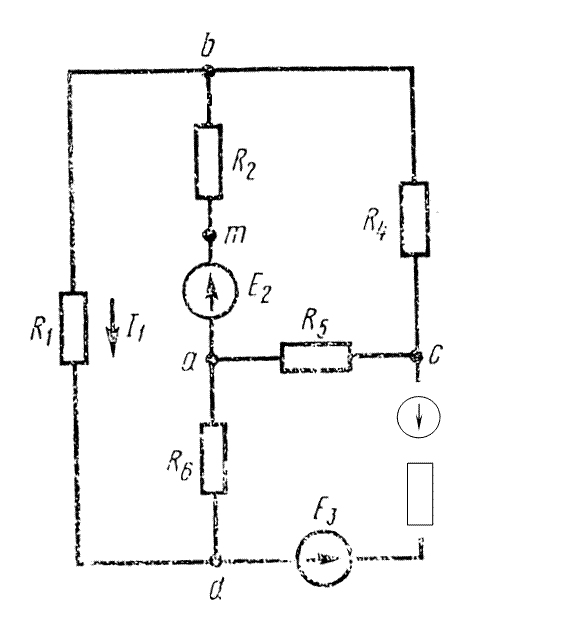Выберем направления контурных токов произвольно.

Число уравнений, которые необходимо составить для расчета токов в ветвях схемы, всегда равно числу независимых контуров. В данной схеме три независимых контура, поэтому имеем следующую систему:

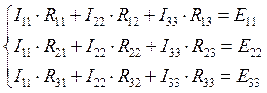
  Контурные токи первого, второго и третьего контуров.

Собственные сопротивления первого, второго и третьего контуров.

Сумма ЭДС первого, второго и третьего контуров. В случае, когда направление ЭДС совпадает с направлением контурного тока, то ЭДС берется со знаком плюс, если не совпадает, то со знаком минус.

Сопротивления с разными индексами – взаимные сопротивления, которые одновременно входят в состав двух контуров. Знак взаимного сопротивления положительный, если направления контурных токов на нем совпадают, в противном случае отрицательный.

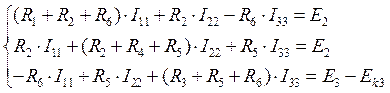
Решим систему матричным способом.

Составим матрицы сопротивлений и ЭДС:

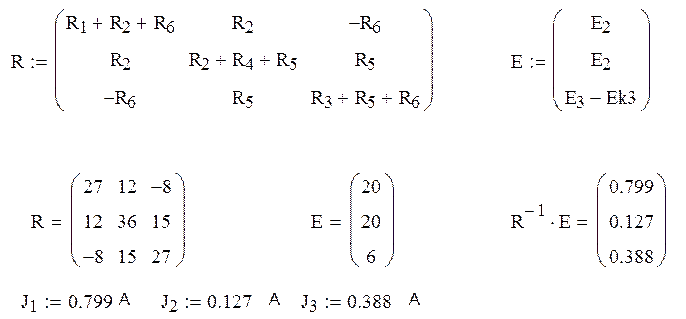
Расчет матрицы производился с помощью программы Mathcad 11 Professional.

Определим истинные токи во всех ветвях цепи:

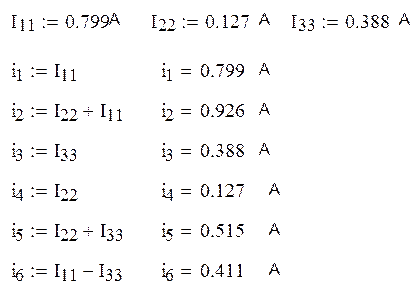
3. Рассчитаем токи во всех ветвях методом узловых потенциалов (МУП).

 

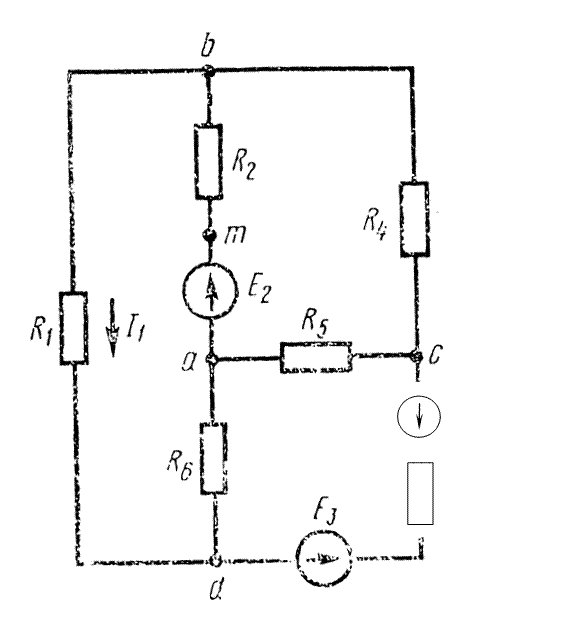Примем в качестве базисного  узел «a» и его потенциал приравняем к нулю φ_a = 0

Остаются неизвестными потенциалы узлов «b», «c», «d»

Вычислим собственные проводимости этих узлов:

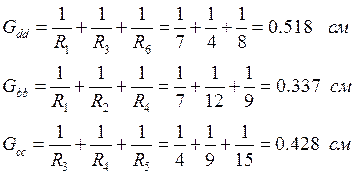
Общая проводимость этих узлов:

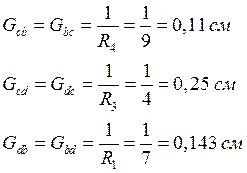
Находим узловые токи:

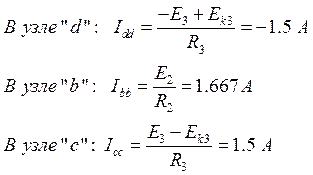
Составим систему уравнений для нахождения потенциалов узлов по методу узловых потенциалов:

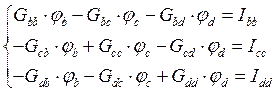
Подставим числовые значения

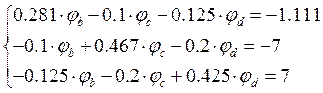
Решим систему матричным способом:

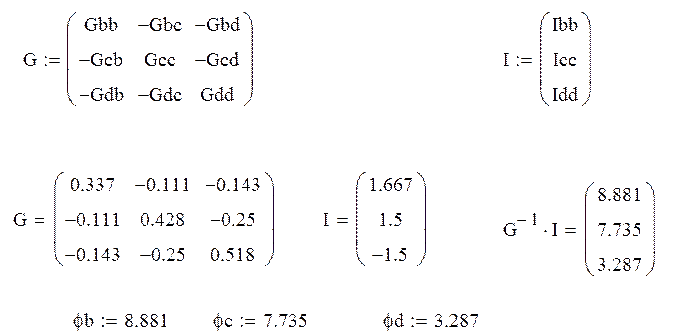
Найдем токи в ветвях:

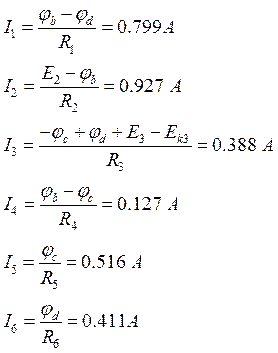
Результаты расчета  токов,  проведенного двумя методами,  сравниваем между собой.

	I1, A	I2, A	I3, A	I4, A	I5, A	I6, A
МКТ	0.799	0.927	0.388	0.127	0.516	0.411
МУП	0.799	0.927	0.388	0.127	0.516	0.411

5. Составить баланс мощностей , вычислить суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).

При  проверке баланса мощностей в тех ветвях цепи, где истинное направление тока совпадает с направлением  ЭДС, соответствующая ЭДС является источником  энергии, а в тех случаях, когда направление ЭДС и тока противоположны, ЭДС – потребитель энергии. Все сопротивления независимо от направления протекающего тока будут являться потребителями энергии.

Суммарная мощность источников:

Суммарная мощность приемников:

Баланс сходится.

6. Определить ток  I₁  в заданной по условию схеме с источником тока методом эквивалентного генератора.

Используя метод эквивалентного генератора, выделяем ветвь