Air to fuel ratio and torque control of spark ignition engines, страница 2

3. Dynamic of air pressure in the intake manifold.

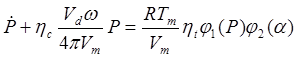                                               (3)

where  is the  intake manifold volume ,  is throttle efficiency,

           

known static functions, ,  are environment pressure and temperature,  is the specific heat ratio,  is the throttle angle (), is the throttle bore diameter. Equation (3) is derived from Ideal Gas Law equation.

4. Fuel to air ratio equation (output)

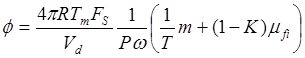                                                         (4)

where  is the fuel to air ratio.

5. Indicated torque equation [7]

.                                                    (5)

Thus mathematical model of spark ignition engine can be presented with nonlinear three-order differential equation with two outputs. Let us rewrite it in terms of control-oriented object (plant).

,                                        (6)

,                                                                                                               (7)

,                                                                                          (8)

,                                                                                                        (9)

                                                                                             (10)

where

control signals:  is the mass flow rate of fuel injected,  is the throttle angle,  is the spark angle (correction signal);

state variables  is the crank speed,  is the mass of fuel film,  is the air pressure in the intake manifold. It is assumed that ,  are measurable;

regulated variables:  is the normalized fuel to air ratio in cylinders,  is the indicated torque.

 is the external load torque (disturbance);

 are corresponding constants which are calculated with the use of equations (1) –(5).

Problem statement can be formulated with the following expressions:

Air to fuel ratio stabilization

.                                                                  (11)

Indicated torque regulation

                                                                (12)

where  is a desired indicated torque.

2. Adaptive air to fuel ratio control

To solve stabilization problem with compensation of uncertain fuel path with the use of adaptive control approach [8, 9].

Thus the model of the air to fuel ratio dynamics is described by equations (7), (9) where parameters of path dynamic , ,  are unknown. The posed control problem will be solved in two steps. First, with the use a special observer we obtain a suitable parametrization (presentation of regulated variable in the linear in unknown parameters form) of model  (7), (9). Then we design an adaptive controller via adaptive technique.

To derive a suitable parametrization  we use the following filters [5]:

,                                                                      (13)

                                                                                (14)

where  is a design parameter. It can be proved that regulated variable can be presented as [5]

                                                                    (15)

where the vector of unknown model parameters  and vector of measurable functions  are defined as

,      .                                                                       (16)

Modifying expressions (15) (16) and introducing control error

,                                                                              (17)

new vectors of controller parameters and measurable functions

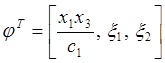,                                        (18)

we obtain the following parametrized model of the control error