define the purpose of control as the solution of the problem of synthesizing the algorithm which at any initial conditions ensures the boundedness of all system signals as well as the execution of purpose condition
, (3)
for some 
, where 
is a tracking error, 
– a number which can be decreased by control law
selection.
3. CONTROL DESIGN
We rewrite the system (1) in the following form
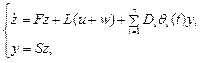(4)
where 
, 
, …, 
- 
vectors; 
, 
, …, 
–components of the vector of unknown time-varying parameters 
.
The state-space model (4) can be represented in the input-output form
(5)
where 
– differentiation operator, transfer function 
.
Before beginning the synthesis of control law let us formulate the auxiliary result published in [14]. Consider linear system time-invariant system
(6)
where 
, 
, 
. Transfer function of system (6) is
determined by expression 
.
Let the system (6) be closed
, (7)
in which number 
.
Let us put a question about
existence of positively defined matrix 
and number 
satisfying the correlations
, (8)
(9)
for some positively defined
matrix 
.
Lemma [14],[15]. Let 
, where 
and 
. Let 
be a Hurwitz polynomial and 
then exists a number 
for which correlations (8), (9) are
solvable for any
.
Choose the control law of the following form
, (10)
where 
is a positive number; the positive parameter 
is intended for compensation of the uncertainties 
and 
; polynomial 
is chosen for the polynomial 
to be Hurwitz and (
) order; function 
is the estimate of signal 
which is calculated according to the following algorithm
(11)
, (12)
where number 
( calculation procedure of 
is presented in Appendix, inequality (A.8)), and parameters 
are calculated for the system (11) to be
asymptotically stable for input 
.
Substituting (10) in equation
we obtain
(13)
where deviation function 
equals
. (14)
Transform the equation (13) in the following way
Let us introduce the
following indication 
,
where according to the
polynomial 
is Hurwitz, parameters 
are bounded and smooth, signal 
and its derivatives up to order 
including we obtain 
is bounded.
Then for equation (13) obtain
.
Let us denote 
, 
,
then for (13) we have
, (15)
where according to the
polynomial is Hurwitz and function 
is bounded we obtain 
is also bounded.
Rewrite the input-output model (15) in state-space form
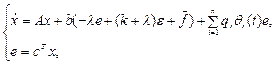(16)
As 
is () order Hurwitz polynomial then in view of
lemma presented above number 
exists that it is possible to find number and symmetrical positively defined matrix 
satisfying following matrix equations
, 
, (17)
where 
is positively defined matrix.
Notice matrix 
parameters depend on parameter and do not depend on .
Let us rewrite model (11), (12) in vector-matrix form
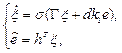(18)
where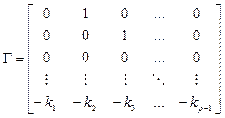 
, 
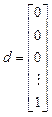and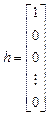 
.
Consider new variable
, (19)
then according the matrix
structure, error 
will
become 
.
For derivative of 
we obtain
. (20)
As 
(can be checked by substitution) then
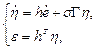(21)
where matrix 
according the calculation of parameters 
of model (11) has proper numbers with negative real
component and satisfies the Lyapunov equation:
, (22)
where 
and 
are positively defined matrixes.
Theorem. There exist numbers and 
such that all trajectories of system (16), (21) are bounded
and control purpose (3) is executed.
The proof of the theorem is presented in Appendix.
4. ADAPTIVE TUNING OF PARAMETERS
In this part we consider the problem of
choosing the controller (10) – (12) parameters 
satisfying the theorem conditions (see expressions (A.4), (A.7) and
(A.8)). Possible variant of tuning the coefficients is to increase them as long as the purpose condition
(3) is executed.
For realization of this idea we use the following algorithm
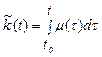, (23)
where 
and function 
is calculated in the following way
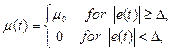where number 
.
Choose 
in the following way
, (24)
where number 
.
It is obvious that with such calculation of
exists a point of time 
for which, condition (17) and inequalities (A.4),
(A.7), (A.8) are executed. It is also evident that tracking error 
will be decreased with the rise of parameter 
(see inequality (A.12)).
5. EXAMPLE
Let us consider the following time-varying plant
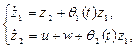(25)
, (26)
where is a measured variable; 
and 
– unknown variable parameters; in contrast
to work [3] we suppose that disturbance affects on the plant, i.e. 
.
Choose control law according to equations (10) – (12)
(27)
, (28)
where polynomial 
and coefficient 
.
To tune the parameters 
and we use the method proposed in the previous part. Assigning the
precision 
and command signal 
we simulate the system for 
and 
. Results of computer simulation for unknown time-varying parameters 
, 
(given parameter values are taken from article [3]) and disturbances 
on variables and 
are presented in the Fig. 1 and 2 accordingly.
Computer simulation graphics for 
and 
illustrate the achievement of proposed control purpose. It is
necessary to note that assigned adaptive control algorithm
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
