Analysis of degeneration of complex dynamic system with human components

AnalySIS of degeneration of complex dynamic system

with human components

Nataliya A. Dudarenko

Department of Control Systems and Informatics

Saint-Petersburg State University of Information Technologies, Mechanics and Optics

Kronversky av. 49, Saint-Petersburg, 197101, RUSSIA

Tel: + 7(812)5954128, E-mail: natasha@cde.ifmo.ru

Abstract – It is concerned the problem of degeneration of complex dynamic system with human components. Problem is solved by functionals of degeneration, constructed with singular values of criterion matrix of complex system. Complex dynamic system with human components is described by interval model representation. 

I.   INTRODUCTION

In this note is concerned the problem of degeneration of complex dynamic system (CDS) with human components. Problem is solved by functionals of degeneration, which are constructed for a complex dynamic system with human components represented by interval model [1]. It’s used descriptions of human operator transfer functions [2], [3] having interval parameters.

For an estimation of degeneration of complex dynamic system is inputted functionals of degeneration that are constructed with singular values of matrix input-output if external influence is determined [4]. Complex dynamic system with human components is described by interval model and therefore functionals of degeneration such system are interval values too.

So, there is problem to estimate corner values of functionals of degeneration that give knowledge about degeneration possibility of CDS.

II.  ESTIMATION OF DEGENERATION OF COMPLEX DYNAMIC SYSTEM. FUNCTIONALS OF DEGENERATION

Given dynamic system in the form of linear algebraic problem (LAP):

,                                                                                                         (1)

where is  matrix for arbitrary ,; ,  is -dimensional vectors,  is -dimensional parameter varying algebraic properties of  .

It’s considered LAP as model tool for checking degeneration. Take a global conditioning value  and separate conditioning values  to estimate degeneration degree of matrix  [5, 6], and determine their in the following form

,                                                    (2)

where , , ,   are the maximum, minimum and - singular conditioning value of matrix  respectively, which take form

,   .                                                              (3)

Conditioning values satisfy to equation [5, 6]

.                                                                                                                     (4)

Consider conversed conditional values, because of difficult to fix infinity, and call their functionals of degeneration  [4], determined in the form

,                                                                              (5)

An addition,

.                                                                                                                      (6)

So, degeneration of LAP (1) can be checked by functionals of degeneration .

III.  MODEL REPRESENTATION OF COMPLEX DYNAMIC SYSTEM WITH HUMAN COMPONENTS

Complex dynamic systems with human components can be two classes:

1.  Competitive class - when human components are involved in technological process with target to find the best individual human component or group of human components;

2.  Creative class - when human components are involved in technological process where target is the best cooperative result.

Degeneration for CDS with human components of first class is the system’s target. Degeneration for CDS with human components of second class is the system’s catastrophe.

Typical human operator transfer function [2, 3] holds:

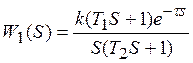,                                                                                                    (7)